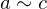Properties of Inverses
- If an element
 has both a left inverse
has both a left inverse 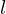 and a right inverse
and a right inverse 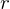 , i.e., if
, i.e., if 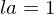 and
and 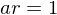 , then
, then 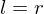 ,
,  is inveritble,
is inveritble, 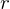 is its inverse
is its inverse - If
 is invertible, its inverse is unique
is invertible, its inverse is unique - Inverses multiply in the opposite order. If
 and
and 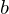 are invertible, so is the product
are invertible, so is the product 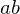 , and
, and 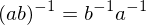 .
. - An element
 may have a left inverse or a right inverse, though it is not invertible.
may have a left inverse or a right inverse, though it is not invertible.
Flashcard set info:
Author: CoboCards-User
Main topic: Mathematics
Topic: Abstract Algebra
School / Univ.: Rice University
City: Houston
Published: 12.02.2017
Tags: Ronan Mukamel
Card tags:
All cards (46)
no tags



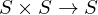


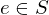
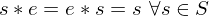
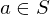 is invertivble if there is a
is invertivble if there is a  s.t.
s.t.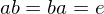
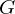 is a set with a law of composition which is
is a set with a law of composition which is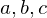 be elements of a group
be elements of a group  or if
or if  then
then  . If
. If 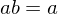 or if
or if 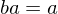 , then b = 1.
, then b = 1.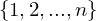 is called the symmetric group and is denoted by
is called the symmetric group and is denoted by 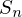 .
. ) denoted
) denoted 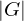
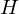 of
of 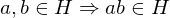 (closed under LOC)
(closed under LOC)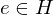 (identity)
(identity)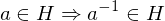 (inverses)
(inverses)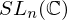
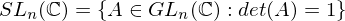
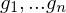 generate
generate  's and
's and 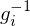 's using LoC.
's using LoC.
 be a subgroup of the additive identity
be a subgroup of the additive identity 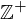 . Either
. Either 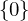 , or else it has the form:
, or else it has the form: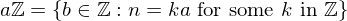
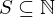 has a least element.
has a least element.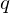 and
and 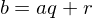 and
and 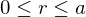
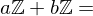 ?
? be their greatest common divisor, the positive integer that generates the subgroup
be their greatest common divisor, the positive integer that generates the subgroup 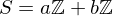 , i.e.
, i.e. 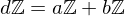 . Then
. Then divides both
divides both  such that
such that 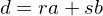
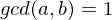
 is a prime integer and divides
is a prime integer and divides 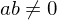 and
and 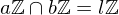 , where
, where 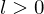 , then
, then  such that
such that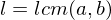
 , then
, then 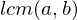 divide
divide 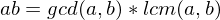
 . The cyclic group generated by
. The cyclic group generated by  is
is
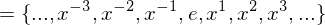
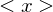 be the cyclic subgroup of
be the cyclic subgroup of 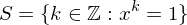 . Then
. Then 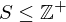
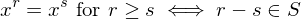
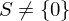 . Then
. Then 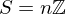 for some
for some 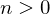 and
and 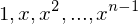 are distinct elements of
are distinct elements of 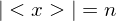 . Then
. Then 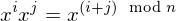 for
for 
 be a regular
be a regular 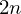 is
is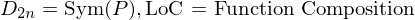

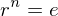
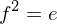
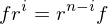
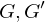 be two groups and
be two groups and 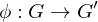 a map of the underlying sets. Then
a map of the underlying sets. Then 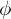 is a homomorphism if
is a homomorphism if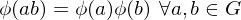
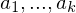 are elements of
are elements of 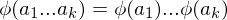
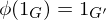
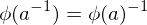
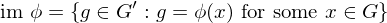
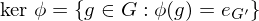
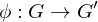 ,
, 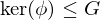 and
and 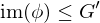
 are group homomorphisms, then
are group homomorphisms, then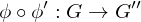 is a group homomorphism.
is a group homomorphism.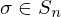 ,
,  be the standard basis vectors for
be the standard basis vectors for 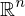 . Then the map from
. Then the map from 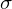 to its permutation matrix is a homomorphism defined as
to its permutation matrix is a homomorphism defined as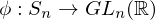

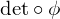 is the sign homomorphism.
is the sign homomorphism.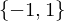
 , a \in G. Then
, a \in G. Then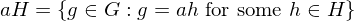
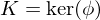 , and
, and 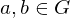 . TFAE:
. TFAE:
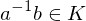
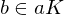
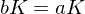

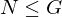 is called normal if
is called normal if 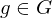 ,
,  implies
implies 
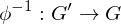 is also an isomorphism
is also an isomorphism of a set
of a set 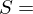 union of disjoint nonempty subsets
union of disjoint nonempty subsets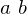 . An equivalence relation is required to be:
. An equivalence relation is required to be: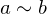 and
and 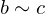 , then
, then