Einheitswurzel
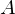 Ring und
Ring und 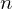 natürliche Zahl mit
natürliche Zahl mit 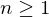 . Ein
. Ein 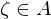 heißt
heißt 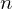 -te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:
-te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:(a)
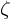 ist Nullstelle des Polynoms
ist Nullstelle des Polynoms 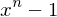
(b) Es ist
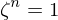
- ist
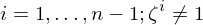 , so heißt
, so heißt 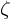 primitiv.
primitiv.-
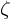 ist Element der Einheitengruppe, insbesondere bilden alle
ist Element der Einheitengruppe, insbesondere bilden alle 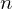 -ten Einheitswurzeln eine Untergruppe der Einheitengruppe.
-ten Einheitswurzeln eine Untergruppe der Einheitengruppe.Faktorieller Ring
Ein Ring 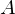 heißt faktoriell, wenn
heißt faktoriell, wenn 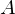 integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
(i) Jede Nicht-Einheit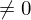 in
in 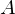 ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen
(ii) Jede Nicht-Einheit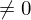 in
in 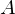 ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
(iii) Es gibt keine unendlichen Teilerketten in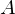 und je zwei Elemente
und je zwei Elemente 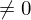 in
in 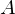 besitzen einen
besitzen einen 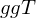 .
.
(iv) Es gibt keine unendlichen Teilerketten in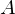 und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.
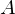 heißt faktoriell, wenn
heißt faktoriell, wenn 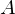 integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:(i) Jede Nicht-Einheit
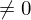 in
in 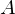 ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen(ii) Jede Nicht-Einheit
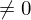 in
in 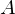 ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.(iii) Es gibt keine unendlichen Teilerketten in
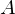 und je zwei Elemente
und je zwei Elemente 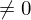 in
in 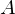 besitzen einen
besitzen einen 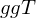 .
.(iv) Es gibt keine unendlichen Teilerketten in
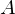 und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.Flashcard set info:
Author: attila.rufius
Main topic: Mathematik
Topic: Algebra
Published: 01.03.2010
Card tags:
All cards (65)
no tags



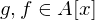
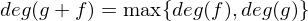
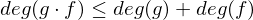 falls
falls 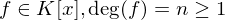 . Eine endliche Erweiterung
. Eine endliche Erweiterung 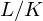 heißt ein Zerfällungskörper von
heißt ein Zerfällungskörper von  , falls
, falls 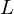 in Linearfaktoren zerfällt, etwa
in Linearfaktoren zerfällt, etwa 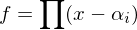
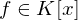 irreduzibel und ist
irreduzibel und ist 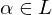 mit
mit 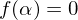 und
und 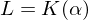 existiert, so heißt
existiert, so heißt 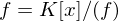 ist ein Wurzelkörper.
ist ein Wurzelkörper.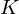 , falls
, falls 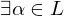 mit
mit 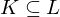 ein Teilkörper.
ein Teilkörper.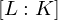 der Körpererweiterung.
der Körpererweiterung.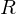 mit
mit 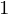 enthält als einzige Ideale
enthält als einzige Ideale 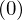 und
und 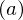 mit
mit 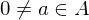 maximal, dann
maximal, dann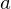 irreduzibel.
irreduzibel.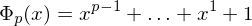 . Es heißt das
. Es heißt das 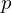 -te Kreisteilungspolynom.
-te Kreisteilungspolynom.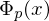 ein Eisensteinpolynom, also irreduzibel.
ein Eisensteinpolynom, also irreduzibel.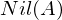 und wovon ist sie der Durchschnitt?
und wovon ist sie der Durchschnitt?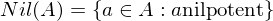 ist genau der Durchschnitt aller Primideale.
ist genau der Durchschnitt aller Primideale.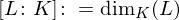 heißt der Grad der Erweiterung.
heißt der Grad der Erweiterung.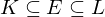 so ist der Grad
so ist der Grad 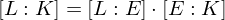
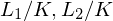 ist eine Abbildung (Ringhomomorphismus)
ist eine Abbildung (Ringhomomorphismus) 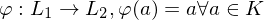 ein
ein 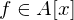 und
und 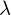 eine Nullstelle in
eine Nullstelle in 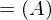 ). Dann ist
). Dann ist 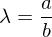 mit
mit 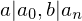
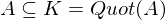 .
. 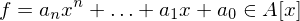 . Gibt es ein
. Gibt es ein 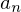 ,
, 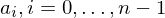 und
und 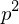 teilt nicht
teilt nicht 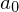 , dan ist
, dan ist 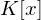 .
.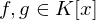 gilt
gilt 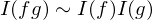 .
.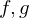 primitiv, so auch
primitiv, so auch 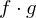 .
.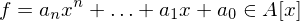 . Gibt es ein Primelement
. Gibt es ein Primelement 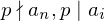 für
für 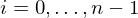 und
und 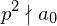 , so ist
, so ist 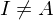 in
in 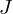 mit
mit 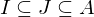 entweder
entweder 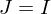 oder
oder 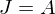 gilt.
gilt.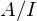 ein Körper ist.
ein Körper ist.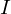 maximal.
maximal.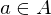 maximal, so ist
maximal, so ist 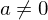 reicht schon aus.
reicht schon aus.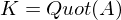 .
.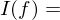 der
der 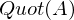 ).
).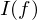 assoziiert zu
assoziiert zu 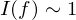 .
.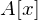 .
.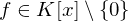 primitiv.
primitiv.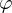 und
und  Ringhomomorphismen,
Ringhomomorphismen, 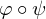 ist...
ist...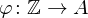 nämlich
nämlich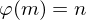 (für alle
(für alle 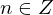 )
) 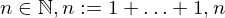 -mal.
-mal. 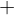 und
und  abgeschlossen, aber...
abgeschlossen, aber...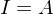 ist.
ist.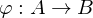 ist der Kern...
ist der Kern...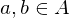 und
und 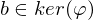 . Also
. Also 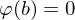 . Mit
. Mit 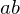 ist
ist 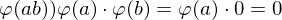 , also
, also 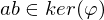 .
.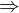
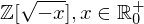 ist die Norm eine Abbildung
ist die Norm eine Abbildung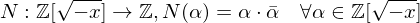
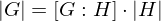
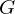 i.Z.
i.Z. 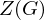 ist die Menge aller derjenigen
ist die Menge aller derjenigen 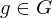 für die gilt:
für die gilt: 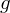 verknüpft mit
verknüpft mit 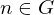 , also
, also 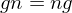 .
.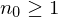 gibt, so dass für alle
gibt, so dass für alle 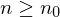 gilt
gilt 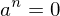 .
.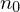 den Nilpotenzindex.
den Nilpotenzindex.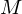 Menge, sei
Menge, sei 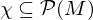 .
.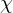 heißt eine Kette, falls für je zwei Elemente aus
heißt eine Kette, falls für je zwei Elemente aus 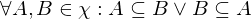
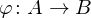 mit den Spektren
mit den Spektren 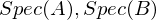 ?
?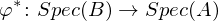 in Gegenrichtung mit
in Gegenrichtung mit 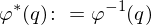 wobei
wobei 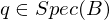 .
. 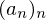 mit
mit 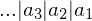
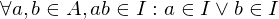
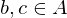 mit
mit 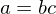 gilt:
gilt: 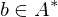 oder
oder 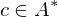 .
.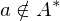 ist und für alle
ist und für alle 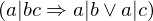 .
.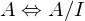 ist Körper
ist Körper 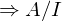 ist integer
ist integer 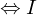 ist prim nach Definition.
ist prim nach Definition.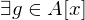 mit
mit 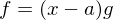 .
.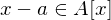 (Leitkoeffizient ist Einheit in
(Leitkoeffizient ist Einheit in 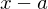 und erhalte Darstellung
und erhalte Darstellung 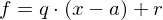 . Einsetzen von
. Einsetzen von 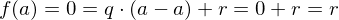
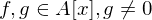 . Ist der Leitkoeffizient von
. Ist der Leitkoeffizient von 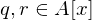 mit
mit 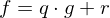 und
und 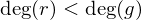 .
.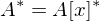
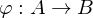 und
und 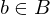 , so gibt es...
, so gibt es...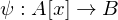 und mit
und mit 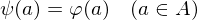 und
und 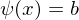 .
.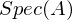 .
.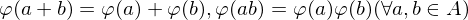 und
und 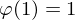 .
.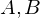 Ringe und
Ringe und 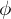 der Ringhomomorphismus von
der Ringhomomorphismus von 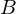 .
.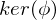 ein Ideal in
ein Ideal in 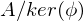 ist isomorph zu
ist isomorph zu 
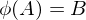 also
also 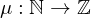 ,
,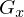 der Stabilisator.
der Stabilisator.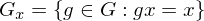
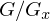 und
und 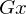 mit
mit 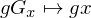 . Ist wohldefiniert.
. Ist wohldefiniert. 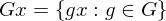
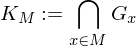 . Falls der Kern nur die Einheit enthält, heißt die Operation treu.
. Falls der Kern nur die Einheit enthält, heißt die Operation treu.