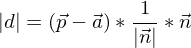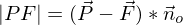Lagebeziehung Gerade - Ebene LGS
LGS
- hat genau eine Lösung -> g schneidet E in genau einem Punkt Richtungsvektoren
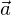 von g ist unabhängig von den Richtungsvektoren der Ebene
von g ist unabhängig von den Richtungsvektoren der Ebene 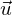 und
und 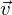
- hat keine Lösung -> g ist parallel zu E -> Richtungsvektoren von g und E sind linear abhängig
- hat unendlich viele Lösungen -> g liegt in E -> Richtungsvektoren von g und E sind linear abhängig
Schnittgerade von zwei Ebene händisch bestimmen
1. LGS aufstellen -> beide Ebenengleichungen gleichsetzen
2. einen beliebigen Parameter für eine Variable einführen
3. Gaußsches Eliminationsverfahren
4. Den Parameter für die Variable in die Ebenengleichung und eine weitere Lösung einsetzten
Beispiel
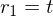
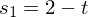
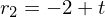
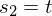 Für
Für 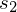 wurde der Parameter t eingeführt
wurde der Parameter t eingeführt
Ebenengleichung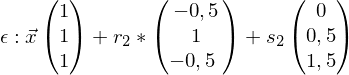
Für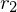 und
und 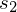 einsetzten
einsetzten
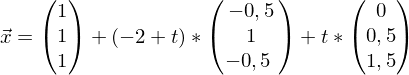
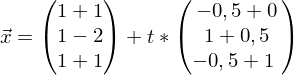
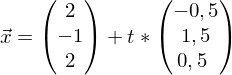
2. einen beliebigen Parameter für eine Variable einführen
3. Gaußsches Eliminationsverfahren
4. Den Parameter für die Variable in die Ebenengleichung und eine weitere Lösung einsetzten
Beispiel
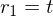
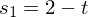
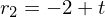
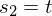 Für
Für 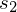 wurde der Parameter t eingeführt
wurde der Parameter t eingeführtEbenengleichung
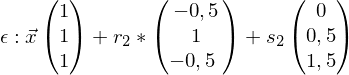
Für
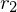 und
und 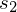 einsetzten
einsetzten 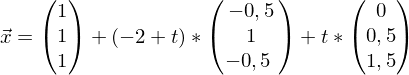
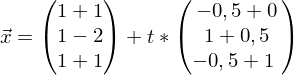
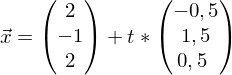
Abstand Gerade - Gerade
- bei Parallelität kann man mit dem Stützvektor der anderen Gerade den Abstand berechnen -> wird zum "Abstandspunkt" der Geraden
Geraden windschief zu einander:
- zwei Ebenengleichungen aufstellen
- Richtungsvektoren der Ebene sind die Richtungsvektoren der zwei Gerade
- Stützvektor ist einmal der von
 und einmal von
und einmal von 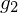 *Abstand Ebene berechnen
*Abstand Ebene berechnen
Flashcard set info:
Author: JamesBond007
Main topic: Mathematik
Topic: Analytische Geometrie
Published: 07.11.2013
Card tags:
All cards (36)
no tags



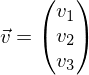


 ist gleich der Strecke
ist gleich der Strecke 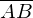
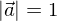 dann wird dieser als Einheitsvektor bezeichnet.
dann wird dieser als Einheitsvektor bezeichnet.
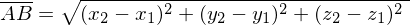
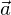 ist genau dann zu einem Vektor
ist genau dann zu einem Vektor 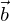 parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt
parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt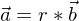 und
und 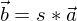
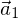 und
und 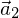 , wenn es reelle Zahlen
, wenn es reelle Zahlen 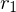 und
und 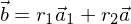 gilt.
gilt.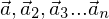 sind
sind 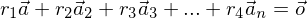 stets
stets
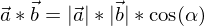 das Skalarprodukt
das Skalarprodukt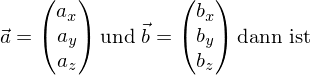
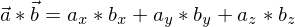
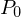 mit dem Stützvektor
mit dem Stützvektor 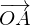 und dem Richtungsvektor
und dem Richtungsvektor 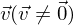 bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung  beschrieben werden.
beschrieben werden. 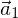 und
und 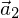 linear abhängig (also parallel) sind.
linear abhängig (also parallel) sind. sein
sein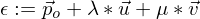
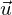 und
und 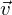 einer Ebene
einer Ebene  orthogonalen Vektor
orthogonalen Vektor 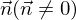 nennt man Normalenvektor von
nennt man Normalenvektor von  . Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit
. Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit 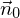 bezeichnet.
bezeichnet. 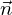 bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung 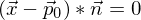 beschrieben werden.
beschrieben werden. 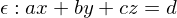

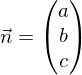
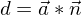 der
der 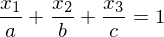

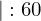
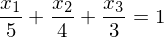
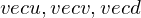 sind linear abhängig
sind linear abhängig


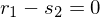

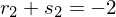
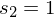
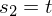 t wird als Parameter für
t wird als Parameter für 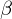 ausrechnen
ausrechnen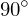 den Winkel
den Winkel 
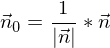
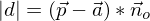 der Vektor
der Vektor