This flashcard is just one of a free flashcard set. See all flashcards!
28
Def.: Toatales Differential
Sei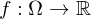 
und 
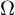ein Gebiet des 
.
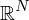Dann heißt
(total) differenzierbar in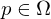 
, falls
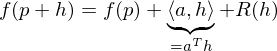
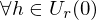
mit einem Vektor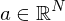
und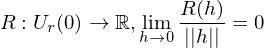 
Wir nennen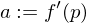
Ableitung von in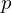 
.
Folgerung
(1) Ist (total) differenzierbar in 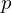, so ist auch stetig in .
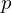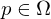
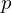(2) Ist in (total) differenziebar, dann auch partiell.
(3) Ist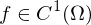
, so ist (total) differenzierbar in .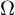
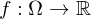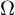und ein Gebiet des 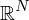.Dann heißt
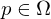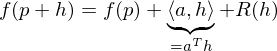
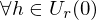
(total) differenzierbar in , fallsmit einem Vektor
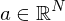und 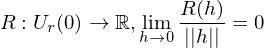Wir nennen
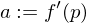Ableitung von in 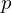.Folgerung
(1) Ist
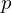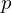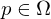
(total) differenzierbar in , so ist auch stetig in . (2) Ist
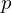in (total) differenziebar, dann auch partiell.(3) Ist
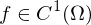, so ist (total) differenzierbar in 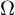.