Def.: Punkte von M
Sei 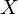 ein metrischer Raum,
ein metrischer Raum, 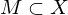 .
.
Ein Punkt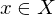 heißt:
heißt:
innerer Punkt von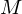 , wenn
, wenn 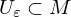 für ein
für ein 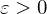
äußerer Punkt von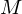 , wenn
, wenn 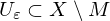 für ein
für ein 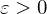
Randpunkt von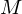 , wenn
, wenn 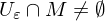 und
und
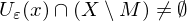 für alle
für alle 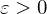
Häufungspunkt von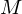 , wenn
, wenn 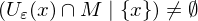 für alle
für alle 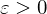
isolierter Punkt von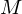 , wenn
, wenn 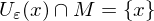 für ein
für ein 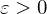 .
. 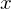 ist kein Häufungspunkt.
ist kein Häufungspunkt.
(z.B. für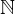 ist jedes
ist jedes 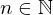 ein isolierter
ein isolierter
Punkt von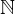 )
)
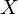 ein metrischer Raum,
ein metrischer Raum, 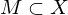 .
. Ein Punkt
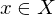 heißt:
heißt:innerer Punkt von
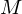 , wenn
, wenn 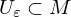 für ein
für ein 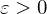
äußerer Punkt von
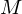 , wenn
, wenn 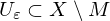 für ein
für ein 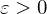
Randpunkt von
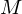 , wenn
, wenn 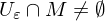 und
und 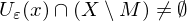 für alle
für alle 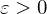
Häufungspunkt von
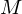 , wenn
, wenn 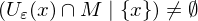 für alle
für alle 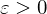
isolierter Punkt von
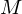 , wenn
, wenn 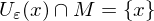 für ein
für ein 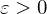 .
. 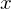 ist kein Häufungspunkt.
ist kein Häufungspunkt. (z.B. für
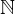 ist jedes
ist jedes 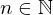 ein isolierter
ein isolierter Punkt von
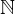 )
)Eigenschaften abgeschlossener Mengen
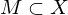 ist abgeschlossen
ist abgeschlossen 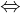 Jeder Häufungspunkt von
Jeder Häufungspunkt von 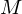 gehört zu
gehört zu 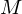 .
.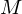 ist abgschlossen genau dann, wenn
ist abgschlossen genau dann, wenn 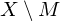 offen ist.
offen ist.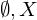 sind abgeschlossen
sind abgeschlossenDer Durchschnitt beliebig vieler abgeschlossener Mengen ist wieder abgeschlossen. Die Vereinigung endlich vieler abgeschlossener Mengen ist wieder abgeschlossen.
Satz über Vollständigkeit von 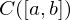
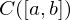
Der unendlichdimensionale normierte Raum 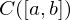 ist vollständig bezüglich
ist vollständig bezüglich
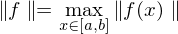
(Maximum- bzw. Supremumnorm auf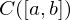 .
.
Bemerkungen
1. Bezüglich der durch das Skalarprodukt
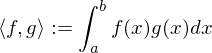
bestimmten Norm ist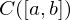 nicht vollständig.
nicht vollständig.
2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge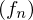 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 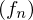 von
von
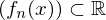
für jedes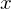 .
.
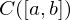 ist vollständig bezüglich
ist vollständig bezüglich 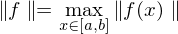
(Maximum- bzw. Supremumnorm auf
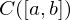 .
.Bemerkungen
1. Bezüglich der durch das Skalarprodukt
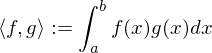
bestimmten Norm ist
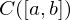 nicht vollständig.
nicht vollständig.2. Konvergenz bezüglich des Maximum heißt auch gleichmäßige Konvergenz der Funktionenfolge
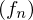 im Gegensatz zur punktweisen Konvergenz der Funktionenfolge
im Gegensatz zur punktweisen Konvergenz der Funktionenfolge 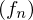 von
von 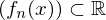
für jedes
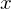 .
.Banachscher Fixpunktsatz
Sei 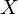 ein vollständig metrischer Raum und
ein vollständig metrischer Raum und  eine Kontraktion auf
eine Kontraktion auf 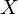 .
.
Dann besitzt in
in 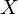 genau einen Fixpunkt
genau einen Fixpunkt 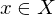 .
.
Dieser ergibt sich durch sukzessive Approximationen:
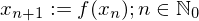
mit beliebigem Startpunkt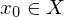 .
.
Bemerkung
Der Fixpunktsatz gilt auch, wenn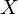 ersetzt wird durch ein abgeschlossenes
ersetzt wird durch ein abgeschlossenes 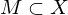 .
.
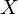 ein vollständig metrischer Raum und
ein vollständig metrischer Raum und  eine Kontraktion auf
eine Kontraktion auf 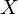 .
. Dann besitzt
 in
in 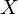 genau einen Fixpunkt
genau einen Fixpunkt 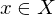 .
.Dieser ergibt sich durch sukzessive Approximationen:
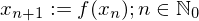
mit beliebigem Startpunkt
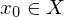 .
.Bemerkung
Der Fixpunktsatz gilt auch, wenn
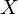 ersetzt wird durch ein abgeschlossenes
ersetzt wird durch ein abgeschlossenes 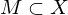 .
.Def.: Toatales Differential
Sei 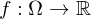 und
und 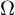 ein Gebiet des
ein Gebiet des 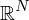 .
.
Dann heißt (total) differenzierbar in
(total) differenzierbar in 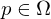 , falls
, falls
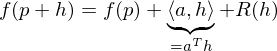
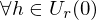
mit einem Vektor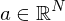 und
und 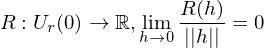
Wir nennen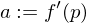 Ableitung von
Ableitung von  in
in 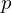 .
.
Folgerung
(1) Ist (total) differenzierbar in
(total) differenzierbar in 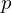 , so ist
, so ist  auch stetig in
auch stetig in 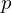 .
. 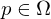
(2) Ist in
in 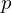 (total) differenziebar, dann auch partiell.
(total) differenziebar, dann auch partiell.
(3) Ist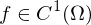 , so ist
, so ist  (total) differenzierbar in
(total) differenzierbar in 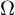 .
.
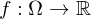 und
und 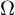 ein Gebiet des
ein Gebiet des 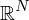 .
.Dann heißt
 (total) differenzierbar in
(total) differenzierbar in 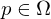 , falls
, falls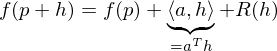
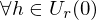
mit einem Vektor
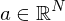 und
und 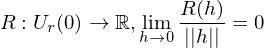
Wir nennen
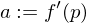 Ableitung von
Ableitung von  in
in 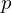 .
.Folgerung
(1) Ist
 (total) differenzierbar in
(total) differenzierbar in 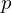 , so ist
, so ist  auch stetig in
auch stetig in 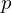 .
. 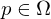
(2) Ist
 in
in 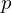 (total) differenziebar, dann auch partiell.
(total) differenziebar, dann auch partiell.(3) Ist
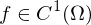 , so ist
, so ist  (total) differenzierbar in
(total) differenzierbar in 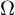 .
.Def.: Vektorfeld
BSP
BSP
Ein Vektorfeld auf 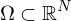 ist eine Abbildung
ist eine Abbildung
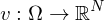
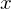
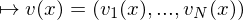
Speziell heißt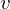 ein
ein 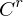 -Vektorfeld auf
-Vektorfeld auf 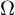 , falls
, falls 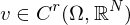 .
.
Integrabilitätsbedingungen
(1) Zwei Stammfunktionen zum Vektorfeld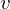 auf einem Gebiet
auf einem Gebiet 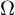 unterscheiden sich nur durch eine Konstante.
unterscheiden sich nur durch eine Konstante.
(2) Dem Vektorfeld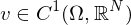 kann eine Differentialform zugeordnet werden:
kann eine Differentialform zugeordnet werden:
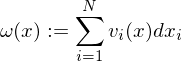
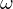 ist exakt wenn gilt:
ist exakt wenn gilt:
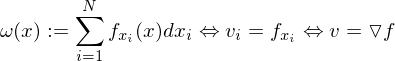
(3) Integrabilitätsbedingung
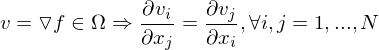
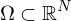 ist eine Abbildung
ist eine Abbildung 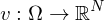
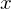
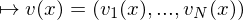
Speziell heißt
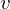 ein
ein 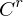 -Vektorfeld auf
-Vektorfeld auf 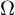 , falls
, falls 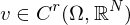 .
.Integrabilitätsbedingungen
(1) Zwei Stammfunktionen zum Vektorfeld
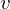 auf einem Gebiet
auf einem Gebiet 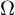 unterscheiden sich nur durch eine Konstante.
unterscheiden sich nur durch eine Konstante.(2) Dem Vektorfeld
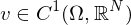 kann eine Differentialform zugeordnet werden:
kann eine Differentialform zugeordnet werden: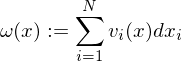
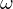 ist exakt wenn gilt:
ist exakt wenn gilt: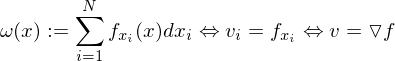
(3) Integrabilitätsbedingung
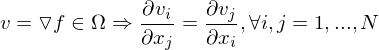
Def.: Diffeomorphismus
Seien 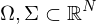 Gebiete.
Gebiete.
Eine Abbildung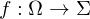 heißt Diffeomorphismus, wenn
heißt Diffeomorphismus, wenn  bijektiv ist und
bijektiv ist und 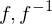 differenzierbar sind.
differenzierbar sind.
 heißt
heißt 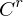 -Diffeomorphismus, falls
-Diffeomorphismus, falls 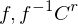 -Abbildungen sind.
-Abbildungen sind.
Man nennt einen lokalen Diffeomorphismus falls es zu jedem
einen lokalen Diffeomorphismus falls es zu jedem 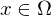 offene Mengen
offene Mengen 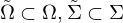 gibt, so dass die Einschränkung
gibt, so dass die Einschränkung 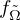 von
von  auf
auf 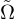 ein Diffeomorphismus von
ein Diffeomorphismus von 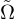 auf
auf 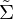 ist.
ist.
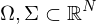 Gebiete.
Gebiete.Eine Abbildung
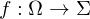 heißt Diffeomorphismus, wenn
heißt Diffeomorphismus, wenn  bijektiv ist und
bijektiv ist und 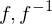 differenzierbar sind.
differenzierbar sind. heißt
heißt 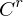 -Diffeomorphismus, falls
-Diffeomorphismus, falls 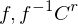 -Abbildungen sind.
-Abbildungen sind.Man nennt
 einen lokalen Diffeomorphismus falls es zu jedem
einen lokalen Diffeomorphismus falls es zu jedem 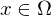 offene Mengen
offene Mengen 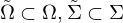 gibt, so dass die Einschränkung
gibt, so dass die Einschränkung 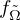 von
von  auf
auf 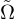 ein Diffeomorphismus von
ein Diffeomorphismus von 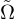 auf
auf 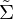 ist.
ist.Absolute Integrierbarkeit
Sei 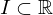 ein offenes oder halboffenes Intervall. Dann heißt
ein offenes oder halboffenes Intervall. Dann heißt  auf
auf 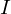 absolut integrierbar, falls
absolut integrierbar, falls
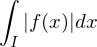
konvergiert oder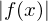 auf
auf 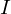 (uneigentlich) Riemann-integrierbar ist.
(uneigentlich) Riemann-integrierbar ist.
Aus absoluter Konvergenz folgt Konvergenz.
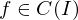 ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
1.Beschränktheitskriterium
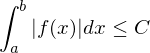
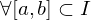
2. Majorantenkriterium
Es existiert eine positive Funktion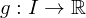 mit
mit
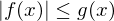
für alle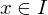 und
und
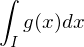
konvergiert.
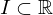 ein offenes oder halboffenes Intervall. Dann heißt
ein offenes oder halboffenes Intervall. Dann heißt  auf
auf 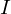 absolut integrierbar, falls
absolut integrierbar, falls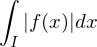
konvergiert oder
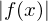 auf
auf 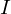 (uneigentlich) Riemann-integrierbar ist.
(uneigentlich) Riemann-integrierbar ist.Aus absoluter Konvergenz folgt Konvergenz.
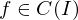 ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:
ist absolut integrierbar genau dann, wenn eine der beiden folgenden Bedingungen erfüllt ist:1.Beschränktheitskriterium
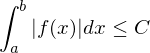
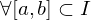
2. Majorantenkriterium
Es existiert eine positive Funktion
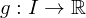 mit
mit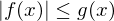
für alle
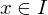 und
und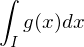
konvergiert.
Flashcard set info:
Author: Schokoholic007
Main topic: Mathematik
Topic: Analysis
Published: 22.04.2010
Card tags:
All cards (53)
no tags



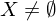 .
.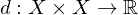 heißt Metrik oder Abstand, falls für alle
heißt Metrik oder Abstand, falls für alle 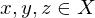 gilt:
gilt: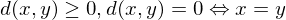
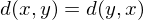
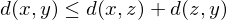
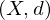 heißt dann metrischer Raum.
heißt dann metrischer Raum.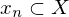 heißt konvergent gegen
heißt konvergent gegen 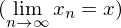 , wenn für alle
, wenn für alle 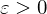 ein
ein 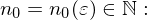
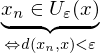
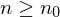
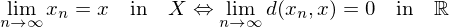
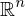 ist äquivalent zur koordinatenweise Konvergenz.
ist äquivalent zur koordinatenweise Konvergenz.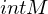 ist die Menge aller inneren Punkte von M.
ist die Menge aller inneren Punkte von M.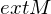 ist die Menge aller äußeren Punkte von M.
ist die Menge aller äußeren Punkte von M.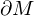 ist die Menge aller Randpunkte von M.
ist die Menge aller Randpunkte von M.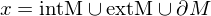
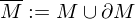 heißt Abschluss oder abgschlossene Hülle von
heißt Abschluss oder abgschlossene Hülle von 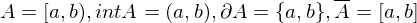
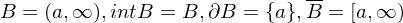
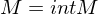
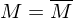
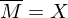
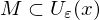
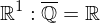 , d.h.
, d.h. 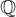 liegt dicht in
liegt dicht in 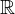
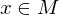 liegt auch
liegt auch 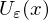 in
in 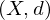 ein metrischer Raum. Dann heißt
ein metrischer Raum. Dann heißt 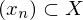 Cauchy-Folge oder Fundamentalfolge, falls für jedes
Cauchy-Folge oder Fundamentalfolge, falls für jedes 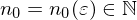 existiert mit
existiert mit 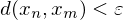 für alle
für alle 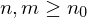 .
.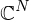 sind vollständig, d.h. sie sind Banachräume bzgl. jeder Norm.
sind vollständig, d.h. sie sind Banachräume bzgl. jeder Norm.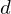 von
von 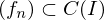 gleichmäßig konvergent gegen f, so ist
gleichmäßig konvergent gegen f, so ist 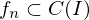 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen 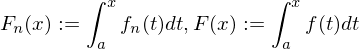
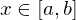 .
. 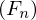 konvergiert gleichmäßig gegen F und
konvergiert gleichmäßig gegen F und 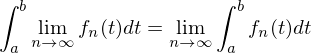
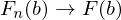 ).
).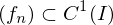 und
und 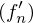 gleichmäßig konvergent gegen
gleichmäßig konvergent gegen 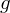 und
und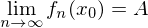 für ein
für ein 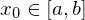 .
.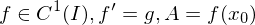 .
.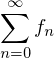
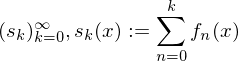
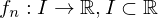 ).
).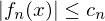 für alle
für alle 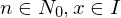 gilt und
gilt und 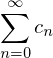
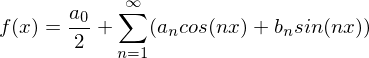
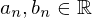
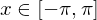
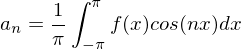
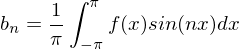
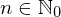
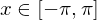 , so auch für alle
, so auch für alle 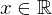
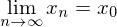
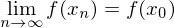 .
.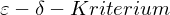 reeler Funktionen)
reeler Funktionen)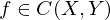
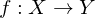 heißt Homöomophismus, falls
heißt Homöomophismus, falls 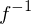 stetig sind.
stetig sind.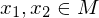 ein
ein 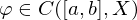 existiert mit
existiert mit 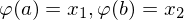 und
und 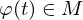 für alle
für alle 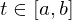 .
.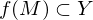 zusammenhängend.
zusammenhängend.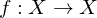 .
.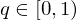 :
: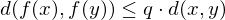
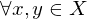
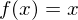 für
für 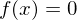 für reelle Funktionen
für reelle Funktionen 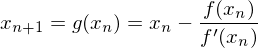
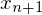 ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.
ensteht durch Schnittpunkt einer Tangente an einem beliebigen Punkt mit der x-Achse.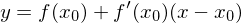
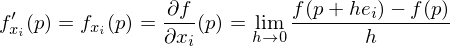
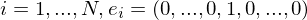 (1 an der i-ten Stelle).
(1 an der i-ten Stelle).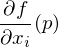 liefert den Anstieg der Fläche y = f(x) in
liefert den Anstieg der Fläche y = f(x) in 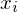 -Richtung und damit den Anstieg der Tangentialebene T.
-Richtung und damit den Anstieg der Tangentialebene T.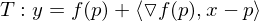
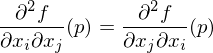
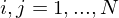
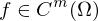 sind die partiellen Ableitungen bis Ordnung
sind die partiellen Ableitungen bis Ordnung 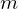 unabhängig von der Differentiationsreihenfolge.
unabhängig von der Differentiationsreihenfolge.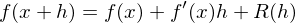
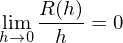 und
und 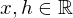 falls
falls 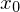 differenzierbar.
differenzierbar.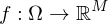
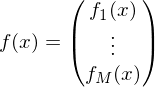
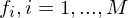 differenzierbar in
differenzierbar in 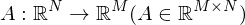
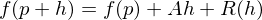
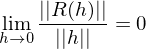
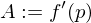 heißt Ableitung von
heißt Ableitung von 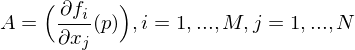
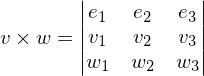
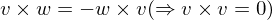
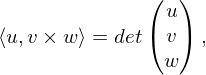
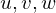 sind Zeilenvektoren.
sind Zeilenvektoren.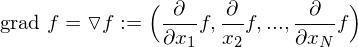
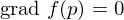 heißen stationäre oder kritische Punkte.
heißen stationäre oder kritische Punkte.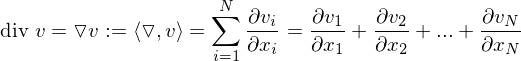
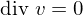 , so heißt das Vektorfeld quellenfrei.
, so heißt das Vektorfeld quellenfrei.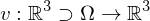
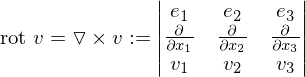
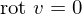 , so heißt das Vektorfeld wirbelfrei.
, so heißt das Vektorfeld wirbelfrei.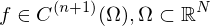 sei ein Gebiet
sei ein Gebiet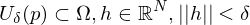 .
.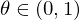 :
: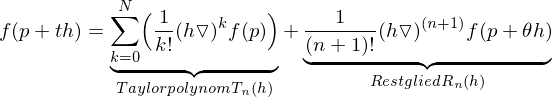
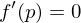
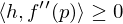
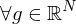
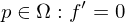 und ist
und ist 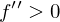
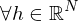 dann hat
dann hat 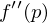 ist positiv definit
ist positiv definit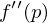 sind positiv
sind positiv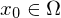
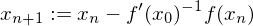
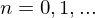
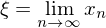 exisiert, so ist
exisiert, so ist 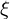 Fixpunkt der Abbildung
Fixpunkt der Abbildung 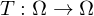 mit
mit 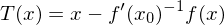 .
.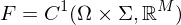 .
. 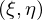 gelte
gelte 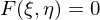 sowie die Auflösebedinung
sowie die Auflösebedinung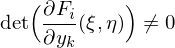 .
.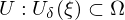 und
und 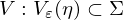 , so dass genau eine stetige Funktion
, so dass genau eine stetige Funktion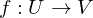 existiert mit
existiert mit 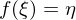 und
und 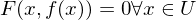 .
.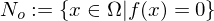
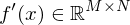
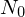 hat die Dimension
hat die Dimension 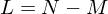
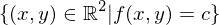 hat die Dimension 1
hat die Dimension 1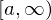 sowie monoton fallend.
sowie monoton fallend.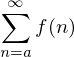
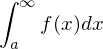
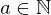 )
)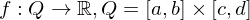
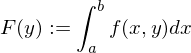
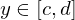 , so heißt
, so heißt 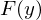 Parametrintegral.
Parametrintegral.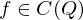 , so existiert
, so existiert 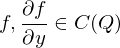 ,
,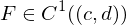 und
und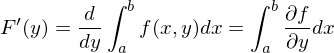
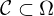 Kurve oder Weg, falls es eine stetige Abbildung
Kurve oder Weg, falls es eine stetige Abbildung 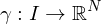
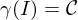 .
.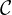 eine
eine 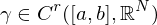
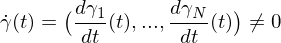
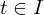 .
.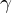 heißt Parametrisierung von
heißt Parametrisierung von 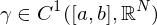 ,
, 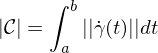
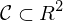 durch eine Funktion
durch eine Funktion 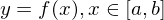 gegeben, so wählt man die Parametrisierung
gegeben, so wählt man die Parametrisierung 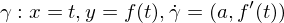 .
.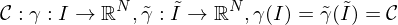
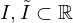 sind Intervalle, heißen äquivalent, wenn es einen
sind Intervalle, heißen äquivalent, wenn es einen 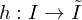 gibt, das heißt
gibt, das heißt 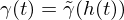 .
.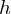 heißt Parametertransformation von
heißt Parametertransformation von 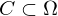 eine reguläre
eine reguläre 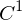 -Kurve mit Parametrisierung, so ist
-Kurve mit Parametrisierung, so ist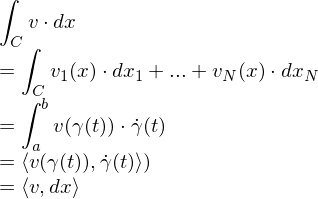
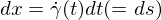 ist vektorielles Bogenelement von
ist vektorielles Bogenelement von 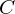 .
.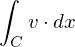
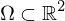 genau dann, wenn
genau dann, wenn 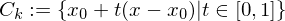 vollständig in
vollständig in 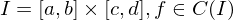 , so gilt
, so gilt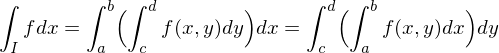
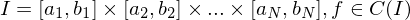 so gilt:
so gilt: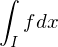
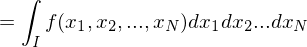
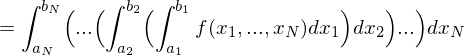
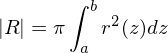
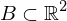 heißt Normalbereich bezüglich er x-Achse, wenn
heißt Normalbereich bezüglich er x-Achse, wenn 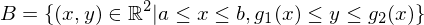
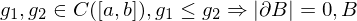 kompakt.
kompakt.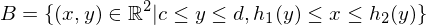
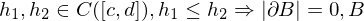 kompakt.
kompakt.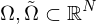 Gebiete und
Gebiete und 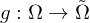 ein
ein 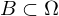 mit
mit 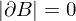 die Formel
die Formel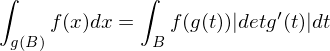
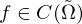
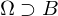 ein Gebiet sowie
ein Gebiet sowie 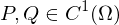 .
.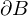 :
: