Was sind die Schritte der LR-Zerlegung für 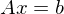 ?
?
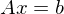 ?
?- Die Matrix A wird in L und R Zerlegt durch Gaussen (ausschliesslich mit Subtraktion) der Matrix A (P Matrix nicht vergessen)
- Danach gilt
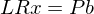
-
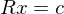 wird zu c zusammengeführt
wird zu c zusammengeführt - Das führt zu
 wo nun nach c aufgelöst werden kann
wo nun nach c aufgelöst werden kann - Mit gefundenem c kann nun für x aufgelöst werden über
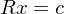
Was sind die Schritte des Gramm-Schmidt Orthogonalisierungsverfahren?
1. Etablierung des ersten Basisvektors: 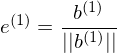
2. Errechnung der Richtung des zweiten Basisvektors:
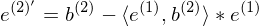
3. Normalisierung des zweiten Basisvektors: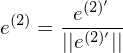
4. Repetition von Schritt 2. und 3. für alle weiter Vektoren der originalen Basis.
Schritt 2. ist jeweils im Schema:
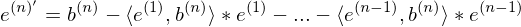
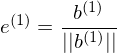
2. Errechnung der Richtung des zweiten Basisvektors:
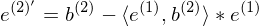
3. Normalisierung des zweiten Basisvektors:
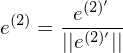
4. Repetition von Schritt 2. und 3. für alle weiter Vektoren der originalen Basis.
Schritt 2. ist jeweils im Schema:
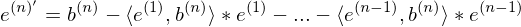
Wie wird die V Matrix der Singulärwertzerlegung errechnet werden?
- Lösen des EWP von
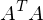
- V ist die Matrix bestehend aus den EV.
- Die Reihenfolge der Matrix korrespondiert zu ihren entsprechenden EW wenn diese vom grössten zum kleinsten geordnet werden.
- V wird orthonormalisiert (mit Gramm-Schmidt)
Wie wird die U Matrix der Singulärwertzerlegung errechnet werden?
- Lösen des EWP von
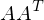
- U ist die Matrix bestehend aus den EV.
- Die Reihenfolge der Matrix korrespondiert zu ihren entsprechenden EW wenn diese vom grössten zum kleinsten geordnet werden.
- U wird orthonormalisiert (mit Gramm-Schmidt)
Flashcard set info:
Author: CoboCards-User
Main topic: Lineare Algebra I
Topic: Lineare Algebra
School / Univ.: ETH Zürich
City: Zürich
Published: 21.01.2020
Tags: 2019
Card tags:
All cards (188)
no tags



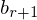 bis
bis 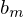 = 0)
= 0)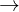 r < n & konsistent
r < n & konsistent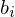 eine Lösung?
eine Lösung?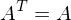
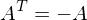
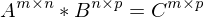
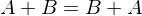
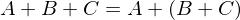

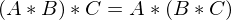
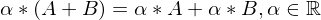
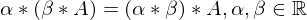
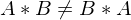
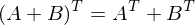
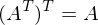
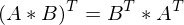
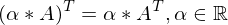
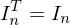
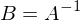
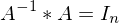
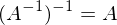
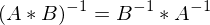
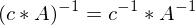
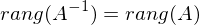
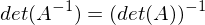
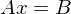 ist
ist 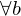 lösbar
lösbar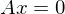 hat nur die triviale Lösung
hat nur die triviale Lösung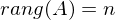
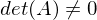
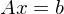 hat entweder keine oder unendlich viele Lösungen
hat entweder keine oder unendlich viele Lösungen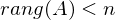
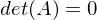
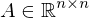
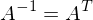
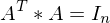
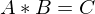 : C ist auch orthogonal wenn A und B orthogonal
: C ist auch orthogonal wenn A und B orthogonal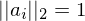 )
)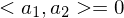
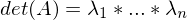
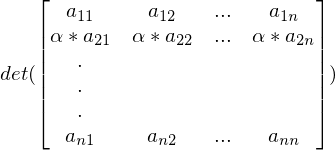
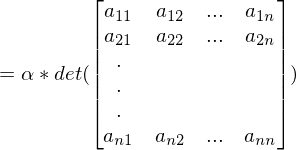
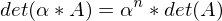
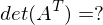
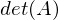
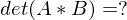
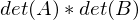
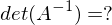
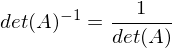
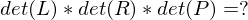
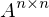 und n ungerade?
und n ungerade?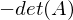
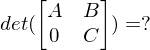
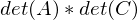
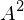 Matrix dar?
Matrix dar?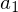 und
und 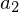
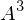 Matrix dar?
Matrix dar?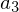 aufgespannt wird (
aufgespannt wird (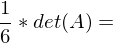 Pyramidenvolumen)
Pyramidenvolumen)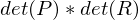
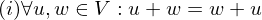
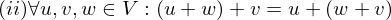
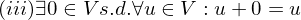
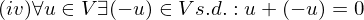
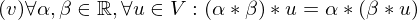
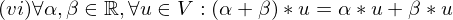
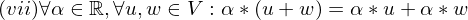
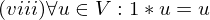

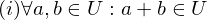
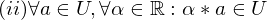
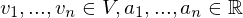 ist gleich
ist gleich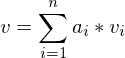
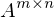 wenn diese erzeugend ist?
wenn diese erzeugend ist?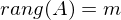
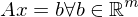 lösbar
lösbar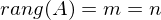
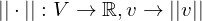
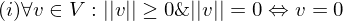
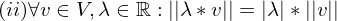
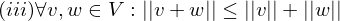
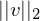 = länge Vektor
= länge Vektor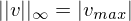 des grössten Eintrages in
des grössten Eintrages in 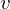
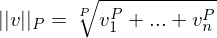
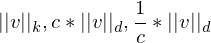 zu ordnen?
zu ordnen?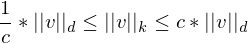
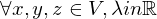
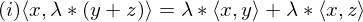
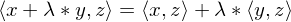
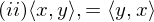
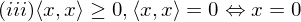 (positive definitheit)
(positive definitheit)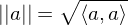
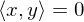 (gilt für jedes Skalarprodukt)
(gilt für jedes Skalarprodukt)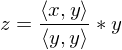
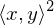
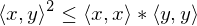
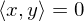
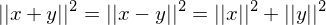 (Pythagoras)
(Pythagoras)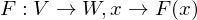
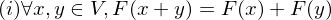
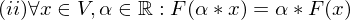
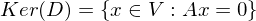
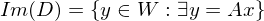
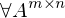
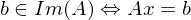 ist ein lösbares LGS
ist ein lösbares LGS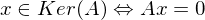
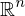
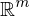
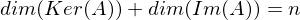
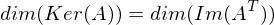
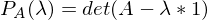
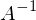 wenn
wenn 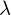 ein Eigenwert von
ein Eigenwert von 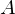 ist.
ist.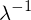
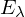 von A zu
von A zu 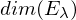 ?
?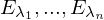 wenn die EV linear unabhängig sind?
wenn die EV linear unabhängig sind?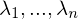 sind paarweise verschieden
sind paarweise verschieden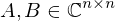 ähnlich?
ähnlich?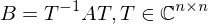
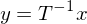
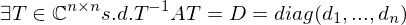
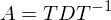
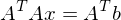
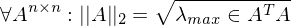
 orthogonale
orthogonale 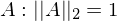
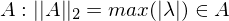
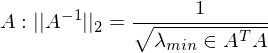
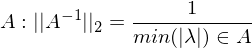
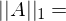 max Spaltensummennorm = Addition des Betrags der Einträge der Spalte
max Spaltensummennorm = Addition des Betrags der Einträge der Spalte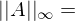 max Zeilensummennorm = Addition des Betrages der Einträge der Zeile
max Zeilensummennorm = Addition des Betrages der Einträge der Zeile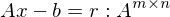 mit
mit 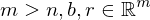
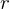
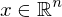 so finden, das
so finden, das 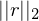 minimal wird.
minimal wird.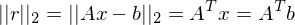
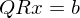
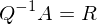
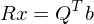
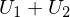 ?
?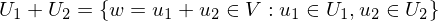
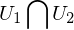
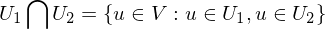
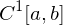 wenn
wenn 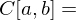 stetige Funktionen}?
stetige Funktionen}?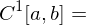 {1 mal diffbare stetige Funktionen}
{1 mal diffbare stetige Funktionen}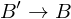 geht?
geht?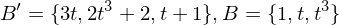
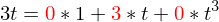
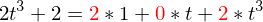
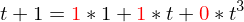
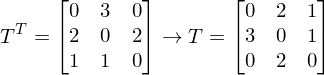
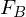 zur Matrix
zur Matrix 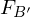 konvertiert werden mit der Übergangsmatrix
konvertiert werden mit der Übergangsmatrix 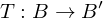
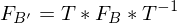
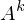 berechnet für A quadratisch und diag-bar?
berechnet für A quadratisch und diag-bar?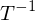 berechnen
berechnen 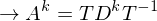
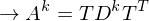
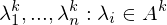
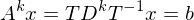 berechnet werden wenn b gesucht ist?
berechnet werden wenn b gesucht ist?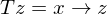 berechnen
berechnen berechnen
berechnen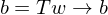 berechnen
berechnen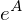 mit einer Summe dargestellt?
mit einer Summe dargestellt?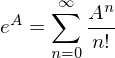
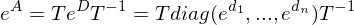
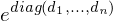 ?
?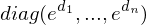
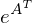 auch dargestellt werden?
auch dargestellt werden?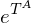
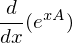 , wenn
, wenn 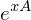 stetig diffbar?
stetig diffbar?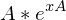
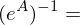
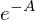
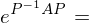
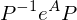
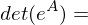
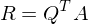
 aus R extrahieren:
aus R extrahieren: 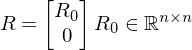
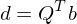
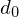 aus d extrahieren:
aus d extrahieren: 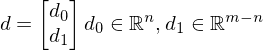
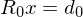
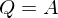
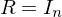
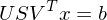
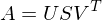
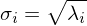 werden vom grössten zum kleinsten auf der Diagonalachse einer
werden vom grössten zum kleinsten auf der Diagonalachse einer 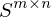 Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
Matrix eingetragen. Alle anderen Werte werden 0 gelassen.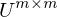
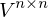
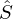 bei der Singulärwertzerlegung der Matrix
bei der Singulärwertzerlegung der Matrix 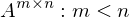
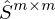
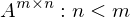
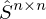
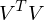
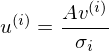 für jeden Vektor in V gerechnet.
für jeden Vektor in V gerechnet.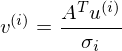 für jeden Vektor in U gerechnet.
für jeden Vektor in U gerechnet.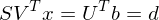
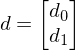 wobei
wobei 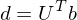
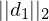
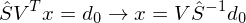
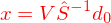
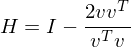
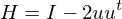
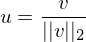
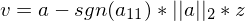
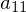 ist der Eintrag der im der oberen linken Ecke auf die die H Matrix angewendet wird
ist der Eintrag der im der oberen linken Ecke auf die die H Matrix angewendet wird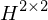 gewählt wenn es aus einer
gewählt wenn es aus einer 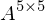 Matrix stammt und angewendet wird
Matrix stammt und angewendet wird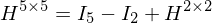
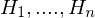 gefunden sind?
gefunden sind?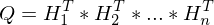
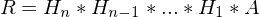
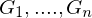 gefunden sind?
gefunden sind?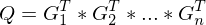
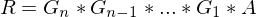
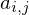 der Matrix
der Matrix 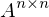 zu Null gemacht werden soll?
zu Null gemacht werden soll?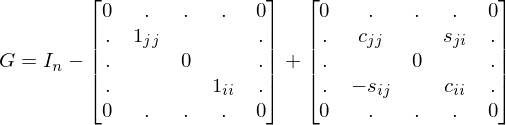
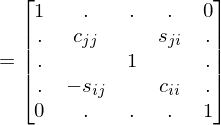
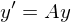 umgeformt werden wenn A diag-bar?
umgeformt werden wenn A diag-bar?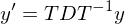
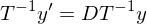
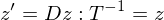
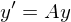
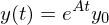
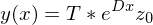 auch geschrieben werden?
auch geschrieben werden?
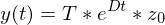
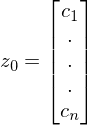
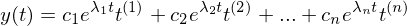
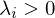
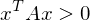
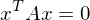 bei einer symmetrischen positiv definiten Matrix A?
bei einer symmetrischen positiv definiten Matrix A?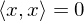 ?
?