Multiplikation: Modellierung als Funktion
Eingabe: zwei binär kodierte Zahlen 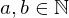
Ausgabe: die binär kodierte Zahl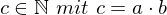
=>es gibt nur eine eindeutige Ausgabe, deshalb Modellierung als Funktion:
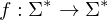 Die zur Eingabe
Die zur Eingabe 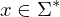 gesuchte Ausgabe ist in diesem Fall
gesuchte Ausgabe ist in diesem Fall 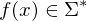 .
.
Führe dazu zum Alphabet ein Trennsymbol # ein: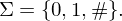
Eingabe ist dann kodiert als: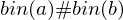
und Ausgabe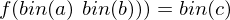
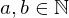
Ausgabe: die binär kodierte Zahl
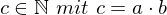
=>es gibt nur eine eindeutige Ausgabe, deshalb Modellierung als Funktion:
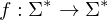 Die zur Eingabe
Die zur Eingabe 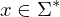 gesuchte Ausgabe ist in diesem Fall
gesuchte Ausgabe ist in diesem Fall 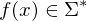 .
.Führe dazu zum Alphabet ein Trennsymbol # ein:
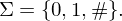
Eingabe ist dann kodiert als:
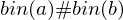
und Ausgabe
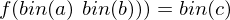
Graphzusammenhang: Modellierung eines Entscheidungsproblems
Eingabe: die Kodierung eines Graphen G =(V,E)
Ausgabe: 1, falls G zusammenhängend. 0, sonst
Kodierung: Als Adjazenzmatrix unter der Annahme, dass diese einen Graph bereits korrekte Kodierung eines Graphen ist
G: Menge aller Graphen
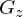 : Menge aller zusammenhängender Graphen
: Menge aller zusammenhängender Graphen
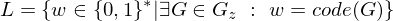
Ausgabe: 1, falls G zusammenhängend. 0, sonst
Kodierung: Als Adjazenzmatrix unter der Annahme, dass diese einen Graph bereits korrekte Kodierung eines Graphen ist
G: Menge aller Graphen
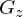 : Menge aller zusammenhängender Graphen
: Menge aller zusammenhängender Graphen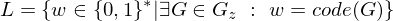
Definition des Turingmachinenmodells
=> man geht von unbeschränkter Rechenzeit und Speicher aus
ist definiert durch das 7-Tupel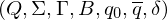
Am Anfang der Rechnung befindet sich die TM im Anfangszustand, auf dem Band steht von links nach rechts die Eingabe in benachbarten Zellen, alle anderen Zellen links und rechts der Eingabe enthalten Leerzeichen, und der Kopf steht unter dem ersten Zeichen der Eingabe.
ist definiert durch das 7-Tupel
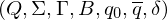
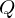 | endliche Zustandsmenge |
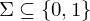 | endliches Eingabealphabet |
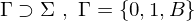 | endliches Bandalphabet |
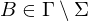 | Blanksymbol |
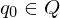 | Anfangszustand |
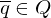 | Stoppzustand |
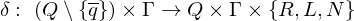 | Zustandsübergangsfunktion |
Rechenschritt
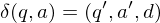
Wenn der aktuelle Zustand der TM q ist und der Kopf auf einer Zelle mit Inhalt a steht, dann schreibt die TM den Buchstaben a', wechselt in den Zustand q' und geht eine Position d=(L,R,N) weiter.
Es wird solange ein Rechenschritt nach dem anderen ausgeführt bis der Stoppzustand
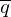 erreicht ist.
erreicht ist.Konfiguration (direkte) Nachfolgekonfiguration
"Schnappschuss" der Rechnung zu einem bestimmten Zeitpunkt
Konfiguration: ist ein String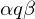 mit
mit 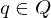 und
und 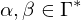
auf dem Band steht eingerahmt von Blanks und der Zustand ist q und der Kopf steht unter dem ersten Zeichen von
eingerahmt von Blanks und der Zustand ist q und der Kopf steht unter dem ersten Zeichen von 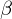
Bsp.: 000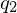 1011 Kopf steht auf rot
1011 Kopf steht auf rot
direkte Nachfolgekonfiguration: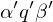 ist d.Nkonf. von
ist d.Nkonf. von 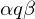 , falls
, falls 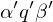 in einem Rechenschritt aus
in einem Rechenschritt aus 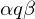 entsteht:
entsteht: 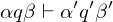
Nachfolgekonfiguration: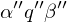 von
von 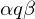 , falls
, falls 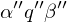 in endlich vielen Rechenschritten aus
in endlich vielen Rechenschritten aus 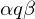 entsteht.
entsteht.
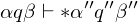
Die Rechnung terminiert, wenn Stoppzustand erreicht ist. Dann gibt es keine Nachfolgekonfiguration.
Konfiguration: ist ein String
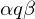 mit
mit 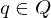 und
und 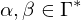
auf dem Band steht
 eingerahmt von Blanks und der Zustand ist q und der Kopf steht unter dem ersten Zeichen von
eingerahmt von Blanks und der Zustand ist q und der Kopf steht unter dem ersten Zeichen von 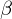
Bsp.: 000
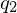 1011 Kopf steht auf rot
1011 Kopf steht auf rotdirekte Nachfolgekonfiguration:
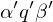 ist d.Nkonf. von
ist d.Nkonf. von 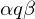 , falls
, falls 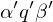 in einem Rechenschritt aus
in einem Rechenschritt aus 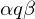 entsteht:
entsteht: 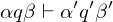
Nachfolgekonfiguration:
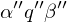 von
von 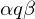 , falls
, falls 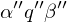 in endlich vielen Rechenschritten aus
in endlich vielen Rechenschritten aus 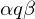 entsteht.
entsteht.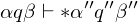
Die Rechnung terminiert, wenn Stoppzustand erreicht ist. Dann gibt es keine Nachfolgekonfiguration.
Wann heißt eine Funktion TM-berechenbar?
Eine TM M, die für alle Eingaben terminiert, berechnet eine totale Funktion 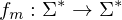 .
.
Da TMs im Allgemeinen nicht immer terminieren berechnen sie also eine Funktion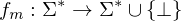
Eine Eingabe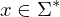 wird auf
wird auf 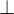 abgebildet, wenn M auf der Eingabe x nicht terminiert. Sonst steht der Kopf im Stoppzustand auf einem Zeichen aus
abgebildet, wenn M auf der Eingabe x nicht terminiert. Sonst steht der Kopf im Stoppzustand auf einem Zeichen aus 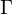 . Wenn das Ergebnis
. Wenn das Ergebnis  ist steht der Kopf auf B.
ist steht der Kopf auf B.
Eine Funktion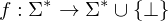 heißt TM-berechenbar, wenn es eine TM M mit
heißt TM-berechenbar, wenn es eine TM M mit 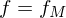 gibt.
gibt.
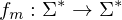 .
.Da TMs im Allgemeinen nicht immer terminieren berechnen sie also eine Funktion
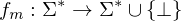
Eine Eingabe
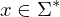 wird auf
wird auf 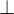 abgebildet, wenn M auf der Eingabe x nicht terminiert. Sonst steht der Kopf im Stoppzustand auf einem Zeichen aus
abgebildet, wenn M auf der Eingabe x nicht terminiert. Sonst steht der Kopf im Stoppzustand auf einem Zeichen aus 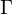 . Wenn das Ergebnis
. Wenn das Ergebnis  ist steht der Kopf auf B.
ist steht der Kopf auf B.Eine Funktion
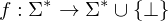 heißt TM-berechenbar, wenn es eine TM M mit
heißt TM-berechenbar, wenn es eine TM M mit 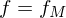 gibt.
gibt. Mehrspur-TM
Bei iner k-spurigen TM, handelt es sich um eine TM, bei der das Band in k Spuren eingeteilt ist.
In jeder Bandzelle stehen k-Zeichen, die der Kopf gleichzeitig lesen kann.
Das Bandalphabet wird also um einen k-dimensionalen Vektor erweitert:
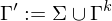
Beispiel: Addition binärer Zahlen: Spur 1 und 2 enthalten zwei binär kodierte Zahlen, das Ergebnis wird auf Spur 3 geschrieben. Überträge werden während der Rechnung im Zustandsraum gespeichert. (3 Phasen!)
In jeder Bandzelle stehen k-Zeichen, die der Kopf gleichzeitig lesen kann.
Das Bandalphabet wird also um einen k-dimensionalen Vektor erweitert:
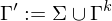
Beispiel: Addition binärer Zahlen: Spur 1 und 2 enthalten zwei binär kodierte Zahlen, das Ergebnis wird auf Spur 3 geschrieben. Überträge werden während der Rechnung im Zustandsraum gespeichert. (3 Phasen!)
Simulation einer k-Band TM M als 1-Band TM M'
Eine k-Band TM M mit Rechenzeit t(n) und Platz s(n), kann von einer 1-Band TM M' mit Zeitbedarf 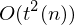 und Platzbedarf O(s(n)) simuliert werden.
und Platzbedarf O(s(n)) simuliert werden.
M' verwendet 2k Spuren:
- ungerade Spuren 1,3,...2k-1 enthalten den Inhalt der Bänder 1...k von M
- gerade Spuren 2,4,...,2k enthalten die Kopfpostitionen von M (mit # markiert)
Die Initialisierung der Spuren ist in konstanter Zeit möglich
Jeder Rechenschritt wird wie folgt simuliert:
- M' geht vom linkesten # bis zum rechtesten # (M' kennt Zustand von M)
- k Zeichen an mit # markierten Positionen werden im Zustandsraum gespeichert (möglich, da nur konstant viele Markierungen)
- M' wertet Übergangsfunktion von M aus (kennt nun neuen Zustand und Bandbewegungen)
- M' läuft zum linkesten # zurück und verändert Bandinschriften und verschiebt # nach links oder rechts.
Laufzeit: Nach t Schritten können die äußeren Markierungen höchstens 2t Positionen auseinander liegen (pro Schritt nur um eine Position verschoben) => Abstand zwischen Zeichen durch O(t(n)) beschränkt => Laufzeit pro Schritt durch O(t(n)) beschränkt => Simulation von t(n) Schritten durch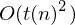 beschränkt
beschränkt
Platzbedarf:linear (zu jeder von M' besuchten Zelle gehört mind. eine Zelle, die M besucht?)
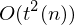 und Platzbedarf O(s(n)) simuliert werden.
und Platzbedarf O(s(n)) simuliert werden.M' verwendet 2k Spuren:
- ungerade Spuren 1,3,...2k-1 enthalten den Inhalt der Bänder 1...k von M
- gerade Spuren 2,4,...,2k enthalten die Kopfpostitionen von M (mit # markiert)
Die Initialisierung der Spuren ist in konstanter Zeit möglich
Jeder Rechenschritt wird wie folgt simuliert:
- M' geht vom linkesten # bis zum rechtesten # (M' kennt Zustand von M)
- k Zeichen an mit # markierten Positionen werden im Zustandsraum gespeichert (möglich, da nur konstant viele Markierungen)
- M' wertet Übergangsfunktion von M aus (kennt nun neuen Zustand und Bandbewegungen)
- M' läuft zum linkesten # zurück und verändert Bandinschriften und verschiebt # nach links oder rechts.
Laufzeit: Nach t Schritten können die äußeren Markierungen höchstens 2t Positionen auseinander liegen (pro Schritt nur um eine Position verschoben) => Abstand zwischen Zeichen durch O(t(n)) beschränkt => Laufzeit pro Schritt durch O(t(n)) beschränkt => Simulation von t(n) Schritten durch
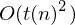 beschränkt
beschränktPlatzbedarf:linear (zu jeder von M' besuchten Zelle gehört mind. eine Zelle, die M besucht?)
universelle TM
simuliert beliebige andere TM M auf beliebiger Eingabe w:
- simuliert das Verhalten von M auf w
- übernimmt das Aktzeptanzverhalten von M
- bei inkorrekter Eingabe (also kein Gödelnummer) Fehlermeldung
- erhält als Eingabe String der Form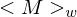 , wobei
, wobei 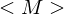 die simulierte TM M kodiert (Gödelnummer)
die simulierte TM M kodiert (Gödelnummer)
- ist im Gegensatz zur normalen TM (special purpose Rechner) general purpose Rechner
- simuliert das Verhalten von M auf w
- übernimmt das Aktzeptanzverhalten von M
- bei inkorrekter Eingabe (also kein Gödelnummer) Fehlermeldung
- erhält als Eingabe String der Form
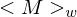 , wobei
, wobei 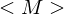 die simulierte TM M kodiert (Gödelnummer)
die simulierte TM M kodiert (Gödelnummer)- ist im Gegensatz zur normalen TM (special purpose Rechner) general purpose Rechner
Gödelnummerierung
- ist injektive Abbildung von der Menge aller TMn in die Menge 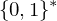
- Präfixfreiheit: keine Gödelnummer darf Anfangsteilwort einer anderen Gödelnummer sein (111 am Ende und nirgends sonst in der Kodierung)
Kodierung:
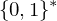
- Präfixfreiheit: keine Gödelnummer darf Anfangsteilwort einer anderen Gödelnummer sein (111 am Ende und nirgends sonst in der Kodierung)
Kodierung:
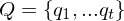 | Menge der Zustände |
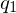 | Anfangszustand (statt 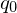 ) ) |
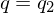 | Stoppzustand |
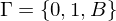 mit mit 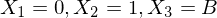 | Bandalphabet durchnummeriert |
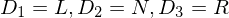 | mögliche Kopfbewegungen durchnummeriert |
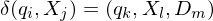 als als 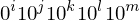 | Übergangsfunktion als Binärstring kodiert |
| <M>= code(1)11code(2)11...11code(s)111 | Kodierung des t-ten Übergangs ist code(t) |
Implementierung der universellen TM als 3-Band-TM
- Band 1: simuliert das Band der TM M
- Band 2: enthält die Gödelnummer von M
- Band 3: enthält den jeweils aktuellen Zustand von M
Initialisierung:
1.) Überprüfung ob Eingabe mit korrekter Göldenummer beginnt (sonst Fehlermeldung)
2.) kopiert <M> auf Band 2
3.) kopiert Binärkodierung des Anfangszustand auf Band 3
4.) kopiert w auf Band 1
5.) Kopf steht auf erstem Zeichen von w
Simulation eines Schritts:
-aktualisiert Inschrift auf Band 1
-bewegt Kopf auf Band 1
-verändert den auf Band 3 abgespeicherten Zustand
Laufzeit:
für Initialisierung O(1) bei konstant angesehener Kodierungslänge
-Laufzeit eines Schritts ist kosntant
=> U simuliert M mit konstantem Zeitverlust
=> wenn wir als 1-Band simulieren quadratischer Zeitverlust
=> konstanter Zeitverlust: wenn GN auf Spur 2 und Zustand auf Spur 3 mit dem Kopf der TM M mitführen(?)
- Band 2: enthält die Gödelnummer von M
- Band 3: enthält den jeweils aktuellen Zustand von M
Initialisierung:
1.) Überprüfung ob Eingabe mit korrekter Göldenummer beginnt (sonst Fehlermeldung)
2.) kopiert <M> auf Band 2
3.) kopiert Binärkodierung des Anfangszustand auf Band 3
4.) kopiert w auf Band 1
5.) Kopf steht auf erstem Zeichen von w
Simulation eines Schritts:
-aktualisiert Inschrift auf Band 1
-bewegt Kopf auf Band 1
-verändert den auf Band 3 abgespeicherten Zustand
Laufzeit:
für Initialisierung O(1) bei konstant angesehener Kodierungslänge
-Laufzeit eines Schritts ist kosntant
=> U simuliert M mit konstantem Zeitverlust
=> wenn wir als 1-Band simulieren quadratischer Zeitverlust
=> konstanter Zeitverlust: wenn GN auf Spur 2 und Zustand auf Spur 3 mit dem Kopf der TM M mitführen(?)
Registermaschine (RAM)
- Speicher ist unbeschränkt und besteht aus Registern 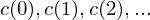
- c(0) ist Akkumulator:
=> Rechenbefehle benutzen ihn als implizites Argument
=> Ergebnis der Rechenoperationen wird dort gespeichert
- Register enthalten beliebig große ganze Zahlen
- Befehlszähler b steht initial auf 1
Eine RAM arbeitet wie ein Programm mit durchnummerierten Befehlen:
- in jedem Schritt wird der Befehl in Programmzeile b abgearbeitet
- goto i: Befehlszähler wird auf i gesetzt
- END stoppt Rechnung
- sonst wird Befehlszähler um eins erhöht
- Eingabe steht am Anfang der Rechnung in den Registern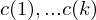
- Ausgabe befindet sich nach dem Stoppen in Registern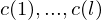
k und l liegen zum Anfang der Rechnung fest.
RAM berechnet Funktion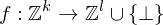
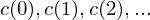
- c(0) ist Akkumulator:
=> Rechenbefehle benutzen ihn als implizites Argument
=> Ergebnis der Rechenoperationen wird dort gespeichert
- Register enthalten beliebig große ganze Zahlen
- Befehlszähler b steht initial auf 1
Eine RAM arbeitet wie ein Programm mit durchnummerierten Befehlen:
- in jedem Schritt wird der Befehl in Programmzeile b abgearbeitet
- goto i: Befehlszähler wird auf i gesetzt
- END stoppt Rechnung
- sonst wird Befehlszähler um eins erhöht
- Eingabe steht am Anfang der Rechnung in den Registern
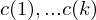
- Ausgabe befindet sich nach dem Stoppen in Registern
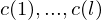
k und l liegen zum Anfang der Rechnung fest.
RAM berechnet Funktion
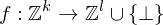
Syntax der RAM (wichtigste, evtl. ergänzen)
| Syntax | Zustandsänderung |
| LOAD i | c(0) := c(i) |
| CLOAD i | c(0) := i |
| STRORE i | c(i) := c(0) |
| ADD i | c(0) := c(0) + c(i) |
| CADD i | c(0) := c(0) + i |
| SUB i | c(0) := c(0) - c(i) |
| CSUB i | c(0) := c(0) - c(i) |
| MULT i | c(0) := c(0) * i |
| CMULT i | c(0) := c(0) * c(i) |
| DIV i | c(0) := Lc(0) / c(i) ┘ |
| CDIV i | Lc(0) / i ┘ |
| GOTO j | b:=j |
| IF c(0) = < <= x GOTO j | b:= j, falls c(0) =<<=x; b+1, sonst |
Simulation RAM durch TM
Simulation der RAM als 2-Band-TM
- ein Band für den Speicher der RAM
- das andere ist Arbeitsband für die TM in den Unterprgrammen
- pro Programmzeile der RAM (p-Stück) ein TM-Unterprogramm
=> ist Unterprogramm für Programmzeile i
ist Unterprogramm für Programmzeile i
-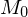 ist Unterprogramm zur Initialisierung der TM
ist Unterprogramm zur Initialisierung der TM
-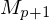 ist Unterprogramm zur Ergebnisaufbereitung
ist Unterprogramm zur Ergebnisaufbereitung
- den Befehlszähler b kann die TM im Zustandsraum abspeichern, da es nur konstant viele Zeilen gibt
- Inhalt der Registern ist allerdings unbeschränkt
=> mit Speicher, Befehlszähler und Unterprogrammen ist die RAM vollständig erfasst.
Rechenschritte:
Rufe durch Befehlszähler b beschriebenes Unterprogramm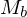 auf
auf
1.)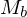 kopiert die in Programmzeile b angesprochenen Register auf Band 1
kopiert die in Programmzeile b angesprochenen Register auf Band 1
2.) führt notwendige Operationen auf Registerinhalten aus
3.) kopiert das Ergebnis des in Programmzeile b angegebenen Registers zurück auf Band 2
4.) aktualisiert Programmzähler
Laufzeit: Länge des Speicherinhalts auf Band 2 ist durch O(n+t(n)) beschränkt, weil die RAM für jedes neue Bit, das sie erzeugt, mindestens eine Zeiteinheit benötigt. Initialisierung benötigt O(n). Laufzeit der Unterprogramme ist polynomiell in Länge der Bandinschrift auf Band 2 beschränkt, also in n+t(n). Gesatmlaufzeit ist also polynomiell in n+t(n) beschränkt.
- ein Band für den Speicher der RAM
- das andere ist Arbeitsband für die TM in den Unterprgrammen
- pro Programmzeile der RAM (p-Stück) ein TM-Unterprogramm
=>
 ist Unterprogramm für Programmzeile i
ist Unterprogramm für Programmzeile i-
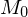 ist Unterprogramm zur Initialisierung der TM
ist Unterprogramm zur Initialisierung der TM-
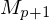 ist Unterprogramm zur Ergebnisaufbereitung
ist Unterprogramm zur Ergebnisaufbereitung- den Befehlszähler b kann die TM im Zustandsraum abspeichern, da es nur konstant viele Zeilen gibt
- Inhalt der Registern ist allerdings unbeschränkt
=> mit Speicher, Befehlszähler und Unterprogrammen ist die RAM vollständig erfasst.
Rechenschritte:
Rufe durch Befehlszähler b beschriebenes Unterprogramm
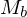 auf
auf1.)
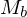 kopiert die in Programmzeile b angesprochenen Register auf Band 1
kopiert die in Programmzeile b angesprochenen Register auf Band 12.) führt notwendige Operationen auf Registerinhalten aus
3.) kopiert das Ergebnis des in Programmzeile b angegebenen Registers zurück auf Band 2
4.) aktualisiert Programmzähler
Laufzeit: Länge des Speicherinhalts auf Band 2 ist durch O(n+t(n)) beschränkt, weil die RAM für jedes neue Bit, das sie erzeugt, mindestens eine Zeiteinheit benötigt. Initialisierung benötigt O(n). Laufzeit der Unterprogramme ist polynomiell in Länge der Bandinschrift auf Band 2 beschränkt, also in n+t(n). Gesatmlaufzeit ist also polynomiell in n+t(n) beschränkt.
Simulation TM durch RAM
Simulation einer 1-Band-TM als RAM:
- Register 1 speichert den Index der Kopfposition
- Register 2 speichert aktuellen Zustand
- Register 3,4,... speichern Inhalte der Bandpositionen 0,1,2,... falls diese zur Eingabe der TM gehören oder vorher vom Kopf besucht wurden
Rechenschritte:
1.) Überprüfung, ob TM im aktuellen Schritt terminiert (falls ja, endet RAM mit entsprechender Ausgabe)
2.) erste Stufe: |Q| viele IF-Abfragen: aktuellen Zustand bestimmen
zweite Stufe: | | viele IF-Abfragen: gelesenes Zeichen bestimmen
| viele IF-Abfragen: gelesenes Zeichen bestimmen
=> je nach Ausgang der IF-Anfragen wird der Zustand in Register 2 und die Kopfposition in Register 1 und das Zeichen an Bandposition c(1) geändert
Laufzeit:
uniformes Kostenmaß: O(n+t(n))
logarithmisches Kostenmaß: Zustände in Zeichen haben konstante Kodierungslänge. Bandpos, die angesprochen werden sind durch n+t(n) beschränkt. Kodierungslänge der Position ist also O(log(n+t(n)). Insgesamt also: O((t(n) + n)log(t(n) + n)
- Register 1 speichert den Index der Kopfposition
- Register 2 speichert aktuellen Zustand
- Register 3,4,... speichern Inhalte der Bandpositionen 0,1,2,... falls diese zur Eingabe der TM gehören oder vorher vom Kopf besucht wurden
Rechenschritte:
1.) Überprüfung, ob TM im aktuellen Schritt terminiert (falls ja, endet RAM mit entsprechender Ausgabe)
2.) erste Stufe: |Q| viele IF-Abfragen: aktuellen Zustand bestimmen
zweite Stufe: |
 | viele IF-Abfragen: gelesenes Zeichen bestimmen
| viele IF-Abfragen: gelesenes Zeichen bestimmen=> je nach Ausgang der IF-Anfragen wird der Zustand in Register 2 und die Kopfposition in Register 1 und das Zeichen an Bandposition c(1) geändert
Laufzeit:
uniformes Kostenmaß: O(n+t(n))
logarithmisches Kostenmaß: Zustände in Zeichen haben konstante Kodierungslänge. Bandpos, die angesprochen werden sind durch n+t(n) beschränkt. Kodierungslänge der Position ist also O(log(n+t(n)). Insgesamt also: O((t(n) + n)log(t(n) + n)
Abzählbare Mengen
Eine Menge M heißt abzählbar, wenn es eine surjektive Funktion  gibt. Nicht abzählbare Mengen heißen überabzählbar.
gibt. Nicht abzählbare Mengen heißen überabzählbar.
Bsp.:
- alle endlichen Mengen sind abzählbar
- Potenzmenge der natürlichen Zahlen ist überabzählbar
- Menge der Sprachen über dem Alphabt {0,1} ist überabzählbar
=> Menge der TMn ist abzählbar (weil durch GN kodierbar und Menge der GN Teilmenge von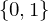
und Menge der Sprachen ist überabzählbar => es gibt mehr Sprachen als TMn
 gibt. Nicht abzählbare Mengen heißen überabzählbar.
gibt. Nicht abzählbare Mengen heißen überabzählbar.Bsp.:
- alle endlichen Mengen sind abzählbar
- Potenzmenge der natürlichen Zahlen ist überabzählbar
- Menge der Sprachen über dem Alphabt {0,1} ist überabzählbar
=> Menge der TMn ist abzählbar (weil durch GN kodierbar und Menge der GN Teilmenge von
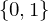
und Menge der Sprachen ist überabzählbar => es gibt mehr Sprachen als TMn
Beweis: D ist nicht rekursiv
Widerspruchsbeweis:
- nehme an D sei rekursiv
- dann gibt es TM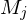 , die D entscheidet
, die D entscheidet
- wende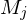 auf
auf 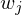 an
an
1.Fall: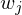 liegt in D
liegt in D
- dann aktzeptiert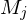 die Eingabe
die Eingabe 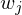 , weil
, weil 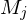 die Sprache entscheidet
die Sprache entscheidet
- Wegen der Definition von D kann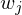 aber nicht in D liegen
aber nicht in D liegen 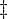
2.Fall: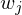 liegt nicht in D
liegt nicht in D
- dann verwirft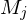 die Eingabe
die Eingabe 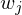 , weil
, weil 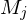 die Sprache entscheidet
die Sprache entscheidet
- Wegen der Definition von D muss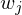 aber in D liegen
aber in D liegen 
- nehme an D sei rekursiv
- dann gibt es TM
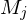 , die D entscheidet
, die D entscheidet- wende
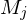 auf
auf 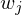 an
an1.Fall:
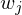 liegt in D
liegt in D- dann aktzeptiert
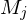 die Eingabe
die Eingabe 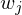 , weil
, weil 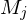 die Sprache entscheidet
die Sprache entscheidet- Wegen der Definition von D kann
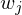 aber nicht in D liegen
aber nicht in D liegen 
2.Fall:
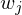 liegt nicht in D
liegt nicht in D- dann verwirft
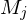 die Eingabe
die Eingabe 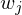 , weil
, weil 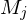 die Sprache entscheidet
die Sprache entscheidet- Wegen der Definition von D muss
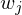 aber in D liegen
aber in D liegen 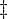
Beweis: L unentscheidbar => 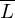 unentscheidbar
unentscheidbar
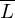 unentscheidbar
unentscheidbarWiderspruchsbeweis:
- nehme an es ex. TM , die
, die 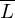 entscheidet
entscheidet
=> hält auf Eingabe w, gdw.
hält auf Eingabe w, gdw. 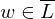
- Konstruiere TM M, die als Unterprogramm aufruft:
als Unterprogramm aufruft:
M startet auf der vorliegenden Eingabe
auf der vorliegenden Eingabe
M negiert Ausgabe von
=> M entscheidet offensichtlich L.
Widerspruch zur Unentscheidbarkeit von L.
=> Komplement der Diagonalsprache ist unentscheidbar
- nehme an es ex. TM
 , die
, die 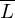 entscheidet
entscheidet=>
 hält auf Eingabe w, gdw.
hält auf Eingabe w, gdw. 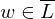
- Konstruiere TM M, die
 als Unterprogramm aufruft:
als Unterprogramm aufruft:M startet
 auf der vorliegenden Eingabe
auf der vorliegenden EingabeM negiert Ausgabe von

=> M entscheidet offensichtlich L.
Widerspruch zur Unentscheidbarkeit von L.
=> Komplement der Diagonalsprache ist unentscheidbar
Beweis: Das Halteproblem ist nicht rekursiv
Zum Zweck des Widerspruchs nehmen wir an, dass H entscheidbar ist. Dann gib es eine TM  , die H entscheidet.
, die H entscheidet.
Konstruieren nun eine TM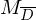 , die
, die  als Unterprgramm aufruft und
als Unterprgramm aufruft und 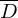 entscheidet.
entscheidet.
(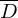 ist unentscheidbar, als kann es
ist unentscheidbar, als kann es  nicht geben)
nicht geben)
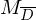 arbeitet wie folgt:
arbeitet wie folgt:
1.) Auf Eingabe w, berechne i, so dass gilt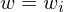
2.) Berechne nun Gödelnummer der i-ten TM: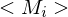
3.) Starte als Unterprogramm auf Eingabe
als Unterprogramm auf Eingabe 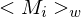
4.) Falls akzeptiert, simuliere
akzeptiert, simuliere  auf w und übernehme deren Akzeptanzverhalten
auf w und übernehme deren Akzeptanzverhalten
5.) Falls verwirft, so verwirf
verwirft, so verwirf
Korrektheit:
1.Fall: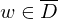 =>
=>  akzeptiert
akzeptiert 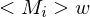 , da
, da  auf w hält=>
auf w hält=>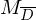 akzeptiert w
akzeptiert w
2.Fall: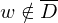 =>
=>  akzeptiert, falls
akzeptiert, falls  w verwirft oder
w verwirft oder  verwirft, falls
verwirft, falls  nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen:
nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen: 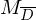 verwirft w.
verwirft w.
 , die H entscheidet.
, die H entscheidet.Konstruieren nun eine TM
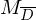 , die
, die  als Unterprgramm aufruft und
als Unterprgramm aufruft und 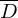 entscheidet.
entscheidet.(
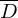 ist unentscheidbar, als kann es
ist unentscheidbar, als kann es  nicht geben)
nicht geben)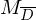 arbeitet wie folgt:
arbeitet wie folgt:1.) Auf Eingabe w, berechne i, so dass gilt
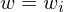
2.) Berechne nun Gödelnummer der i-ten TM:
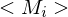
3.) Starte
 als Unterprogramm auf Eingabe
als Unterprogramm auf Eingabe 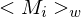
4.) Falls
 akzeptiert, simuliere
akzeptiert, simuliere  auf w und übernehme deren Akzeptanzverhalten
auf w und übernehme deren Akzeptanzverhalten5.) Falls
 verwirft, so verwirf
verwirft, so verwirfKorrektheit:
1.Fall:
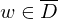 =>
=>  akzeptiert
akzeptiert 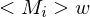 , da
, da  auf w hält=>
auf w hält=>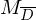 akzeptiert w
akzeptiert w2.Fall:
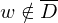 =>
=>  akzeptiert, falls
akzeptiert, falls  w verwirft oder
w verwirft oder  verwirft, falls
verwirft, falls  nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen:
nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen: 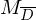 verwirft w.
verwirft w.spezielles Halteproblem
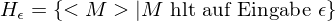
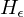 ist nicht rekursiv, aber rekursiv aufz.
ist nicht rekursiv, aber rekursiv aufz. (Eine TM
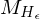 , die
, die 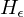 erkennt, aktzeptiert als Eingabe nur TMs, die auf Epsilon halten, TMs die dies nicht tun, halten also nie auf Eingabe Epsilon und damit muss
erkennt, aktzeptiert als Eingabe nur TMs, die auf Epsilon halten, TMs die dies nicht tun, halten also nie auf Eingabe Epsilon und damit muss 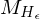 darauf auch nicht halten.)
darauf auch nicht halten.)=>
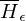 ist nicht rekursiv aufz. (andernfalls wäre
ist nicht rekursiv aufz. (andernfalls wäre 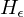 rekursiv)
rekursiv)Beweis: spezielles Halteproblem ist nicht rekursiv
Zum Zwecke des Widerspruchs nehmen wir an, dass 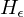 entscheidbar ist. Es gibt also eine TM
entscheidbar ist. Es gibt also eine TM  , die
, die 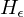 entscheidet.
entscheidet.
Konstruieren nun eine TM , die
, die  als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann
als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann  also nicht ex.)
also nicht ex.)
Die TM arbeiten wie folgt:
arbeiten wie folgt:
1.) Falls die Eingabe keine korrekte GN ist, verwirft die Eingabe
die Eingabe
2.) sonst, auf alle Eingaben der Form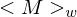 berechnet
berechnet  die GN einer TM
die GN einer TM 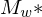 mit folgenden Eigenschaften:
mit folgenden Eigenschaften:
- falls die TM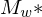 auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.
auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.
- auf anderen Eingaben, verhält sie sich beliebig
3.) schreibt GN
schreibt GN 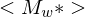 aufs Band und startet
aufs Band und startet  auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.
auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.
Korrektheit:
1.Fall: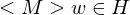 => M hält auf w =>
=> M hält auf w => 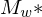 hält auf
hält auf  , da sonst M auf w nicht simuliert worden wäre =>
, da sonst M auf w nicht simuliert worden wäre => 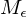 akzeptiert
akzeptiert 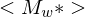 =>
=> akzeptiert
akzeptiert 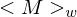
2. Fall: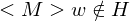 => M hält nicht auf w =>
=> M hält nicht auf w => 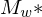 hält nicht auf
hält nicht auf  =>
=>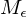 verwirft
verwirft 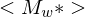 =>
=>  verwirft
verwirft 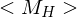
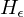 entscheidbar ist. Es gibt also eine TM
entscheidbar ist. Es gibt also eine TM  , die
, die 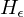 entscheidet.
entscheidet.Konstruieren nun eine TM
 , die
, die  als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann
als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann  also nicht ex.)
also nicht ex.)Die TM
 arbeiten wie folgt:
arbeiten wie folgt:1.) Falls die Eingabe keine korrekte GN ist, verwirft
 die Eingabe
die Eingabe2.) sonst, auf alle Eingaben der Form
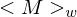 berechnet
berechnet  die GN einer TM
die GN einer TM 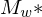 mit folgenden Eigenschaften:
mit folgenden Eigenschaften:- falls die TM
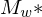 auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.
auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.- auf anderen Eingaben, verhält sie sich beliebig
3.)
 schreibt GN
schreibt GN 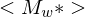 aufs Band und startet
aufs Band und startet  auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.
auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.Korrektheit:
1.Fall:
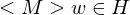 => M hält auf w =>
=> M hält auf w => 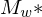 hält auf
hält auf  , da sonst M auf w nicht simuliert worden wäre =>
, da sonst M auf w nicht simuliert worden wäre => 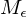 akzeptiert
akzeptiert 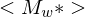 =>
=> akzeptiert
akzeptiert 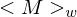
2. Fall:
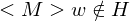 => M hält nicht auf w =>
=> M hält nicht auf w => 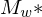 hält nicht auf
hält nicht auf  =>
=>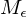 verwirft
verwirft 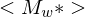 =>
=>  verwirft
verwirft 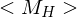
Satz von Rice
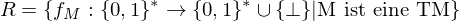
R bezeichnet also die Menge der TM-berechenbaren Funktionen.
Sei S eine Teilmenge von R mit
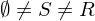 . Dann ist die Sprache
. Dann ist die Sprache  nicht rekursiv.
nicht rekursiv.Nicht-triviale Eigenschaften der von einer TM berechneten Funktion sind nicht entscheidbar.
Konsequenzen für die Praxis: Es kann keinen Compiler geben, der entscheidet, ob ein gegebenes TM oder RAM_Programm auf allen Eingaben terminiert, weil der Compiler dazu entscheiden müsste, ob das Programm eine Funktion der Form
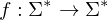 berechnet
berechnetBeweis: Satz von Rice
Unterprogrammtechnik:
Sei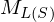 eine TM, die L(S) entscheidet. Konstruiere eine TM
eine TM, die L(S) entscheidet. Konstruiere eine TM 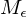 , die
, die 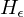 entscheidet und
entscheidet und 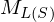 als Unterprogramm aufruft. (Widerspruch zu
als Unterprogramm aufruft. (Widerspruch zu 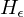 unentscheidbar)
unentscheidbar)
Sei u die überall undefinierte Funktion.
1. Fall: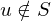
Sei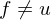 eine Funktion aus S. (Ex. aufgrund Vors.
eine Funktion aus S. (Ex. aufgrund Vors. 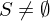 ). Die TM
). Die TM 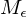 arbeitet so:
arbeitet so:
1.) Eingabe keine korrekte GN <M>: verwirft die Eingabe
2.) Konstruiere aus der GN <M> eine TM M* mit folgendem Verhalten:
(a) Ignoriere die Eingabe x. Simuliere M auf Eingabe auf einer dafür reservierten Spur (von M*).
auf einer dafür reservierten Spur (von M*).
(b) Berechne f(x), simuliere M auf Eingabe x.
=> M* berechnet also nur f(x), wenn M in Schritt (a) auf gehalten hat.
gehalten hat.
3.)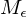 startet
startet 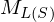 auf <M*> und akzeptert, wenn
auf <M*> und akzeptert, wenn 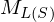 akzeptiert.
akzeptiert.
Sei
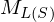 eine TM, die L(S) entscheidet. Konstruiere eine TM
eine TM, die L(S) entscheidet. Konstruiere eine TM 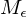 , die
, die 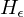 entscheidet und
entscheidet und 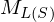 als Unterprogramm aufruft. (Widerspruch zu
als Unterprogramm aufruft. (Widerspruch zu 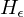 unentscheidbar)
unentscheidbar)Sei u die überall undefinierte Funktion.
1. Fall:
Sei
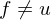 eine Funktion aus S. (Ex. aufgrund Vors.
eine Funktion aus S. (Ex. aufgrund Vors. 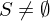 ). Die TM
). Die TM 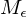 arbeitet so:
arbeitet so:1.) Eingabe keine korrekte GN <M>: verwirft die Eingabe
2.) Konstruiere aus der GN <M> eine TM M* mit folgendem Verhalten:
(a) Ignoriere die Eingabe x. Simuliere M auf Eingabe
 auf einer dafür reservierten Spur (von M*).
auf einer dafür reservierten Spur (von M*).(b) Berechne f(x), simuliere M auf Eingabe x.
=> M* berechnet also nur f(x), wenn M in Schritt (a) auf
 gehalten hat.
gehalten hat.3.)
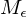 startet
startet 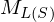 auf <M*> und akzeptert, wenn
auf <M*> und akzeptert, wenn 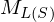 akzeptiert.
akzeptiert.Beweis: Satz von Rice Korrektheit
Korrektheit:
Falls Eingabe keine Korrekt GN ist, verwirft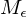 korrekterweise die Eingabe. Bei Eingaben der Form
korrekterweise die Eingabe. Bei Eingaben der Form  gilt:
gilt:
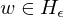 :
:
=> M hält auf
=> M* berechnet f
=> <M*>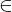 L(S)
L(S)
=>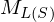 akzeptiert <M*>
akzeptiert <M*>
=>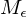 akzeptiert w
akzeptiert w
 :
:
=> M hält nicht auf
=> M* berechnet u
=>
=>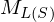 verwirft <M*>
verwirft <M*>
=>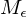 verwirft w.
verwirft w.
2.Fall: wähle f aus
wähle f aus 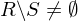
Falls Eingabe keine Korrekt GN ist, verwirft
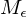 korrekterweise die Eingabe. Bei Eingaben der Form
korrekterweise die Eingabe. Bei Eingaben der Form  gilt:
gilt: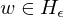 :
:=> M hält auf

=> M* berechnet f
=> <M*>
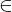 L(S)
L(S)=>
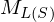 akzeptiert <M*>
akzeptiert <M*>=>
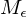 akzeptiert w
akzeptiert w :
: => M hält nicht auf

=> M* berechnet u
=>

=>
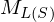 verwirft <M*>
verwirft <M*>=>
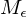 verwirft w.
verwirft w.2.Fall:
 wähle f aus
wähle f aus 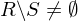
Aufzähler
- Variante einer TM mit angeschlossenem Drucker (zusätzliches Ausgabeband, auf dem sich der Kopf nur nach rechts bewegt)
- ennummeriert alle Wörter aus L auf dem Drucker
1.) gedruckt werden nur Wörter aus L
2.) jedes Wort aus L wird irgendwann ausgegeben
=> Wiederholen der Wörter ist nicht explizit verboten
=> eine Sprache heißt rekursiv aufzählbar, wenn es einen Aufzähler L gibt.
- ennummeriert alle Wörter aus L auf dem Drucker
1.) gedruckt werden nur Wörter aus L
2.) jedes Wort aus L wird irgendwann ausgegeben
=> Wiederholen der Wörter ist nicht explizit verboten
=> eine Sprache heißt rekursiv aufzählbar, wenn es einen Aufzähler L gibt.
semi-entscheidbar/rekursiv aufzählbar
Eine Sprache L ist genau dann semi-entscheidbar, wenn L rekursiv aufzählbar ist
Beweis:
"<=": Konstruiere aus einem Auzähler für L eine TM M, die L erkennt
- zusätzliche Spur, die Rolle des Drucker übernimmt
- wenn neues Wort enummeriert wurde, vergleicht es M mit w
- falls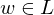 wird w irgendwann enummeriert und von M akzeptiert
wird w irgendwann enummeriert und von M akzeptiert
- falls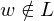 wird w nicht akzeptiert, aber M hält auch nicht
wird w nicht akzeptiert, aber M hält auch nicht
"=>": Konstruiere aus eine TM M, die L erkennt einen Aufzähler
- führe i Schritte von M auf Wörtern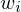 aus (kanonische Reihenfolge)
aus (kanonische Reihenfolge)
- wird ein Wort akzeptiert, drucke es aus
- falls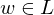 wird L nach endlich vielen Schritten gedruckt
wird L nach endlich vielen Schritten gedruckt
- falls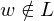 wird w nie gedruckt
wird w nie gedruckt
Beweis:
"<=": Konstruiere aus einem Auzähler für L eine TM M, die L erkennt
- zusätzliche Spur, die Rolle des Drucker übernimmt
- wenn neues Wort enummeriert wurde, vergleicht es M mit w
- falls
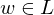 wird w irgendwann enummeriert und von M akzeptiert
wird w irgendwann enummeriert und von M akzeptiert- falls
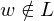 wird w nicht akzeptiert, aber M hält auch nicht
wird w nicht akzeptiert, aber M hält auch nicht"=>": Konstruiere aus eine TM M, die L erkennt einen Aufzähler
- führe i Schritte von M auf Wörtern
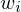 aus (kanonische Reihenfolge)
aus (kanonische Reihenfolge)- wird ein Wort akzeptiert, drucke es aus
- falls
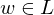 wird L nach endlich vielen Schritten gedruckt
wird L nach endlich vielen Schritten gedruckt- falls
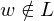 wird w nie gedruckt
wird w nie gedruckt Beweis: Wenn Sprachen 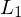 und
und 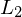 rekursiv (aufzählbar), dann auch
rekursiv (aufzählbar), dann auch 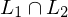 rekursiv (aufzählbar)
rekursiv (aufzählbar)
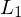 und
und 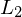 rekursiv (aufzählbar), dann auch
rekursiv (aufzählbar), dann auch 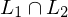 rekursiv (aufzählbar)
rekursiv (aufzählbar)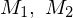 zwei TMn, die
zwei TMn, die 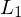 bzw.
bzw. 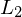 entscheiden (erkennen).
entscheiden (erkennen).Konstruieren eine TM M, die
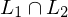 entscheidet (erkennt)
entscheidet (erkennt)- simuliere das Verhalten von
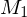 auf w, dann das Verhalten von
auf w, dann das Verhalten von 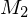 auf w
auf w- Falls
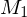 und
und 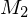 akzeptieren, so auch M
akzeptieren, so auch M=> M akzeptiert offensichtlich die Eingaben von
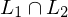 , da sowohl
, da sowohl 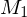 als auch
als auch 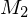 auf jeder Eingabe halten. Also entscheidet (erkennt) M die Sprache
auf jeder Eingabe halten. Also entscheidet (erkennt) M die Sprache 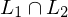 .
.Beweis: Wenn Sprachen 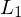 und
und 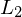 rekursiv, dann auch ihre Vereinigung
rekursiv, dann auch ihre Vereinigung 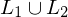 rekursiv
rekursiv
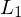 und
und 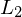 rekursiv, dann auch ihre Vereinigung
rekursiv, dann auch ihre Vereinigung 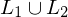 rekursiv
rekursiv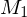 und
und 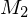 TMn, die
TMn, die 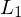 bzw.
bzw. 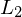 entscheiden.
entscheiden.Konstruiere eine TM M, die
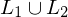 entscheidet:
entscheidet:- Simuliere das Verhalten von
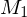 auf w, danach das von
auf w, danach das von 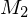 auf w
auf w- Falls
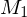 oder
oder 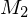 akzeptieren, so auch M.
akzeptieren, so auch M.=> M akzeptiert offensichtlich alle Eingaben aus
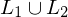 , da sowohl
, da sowohl 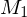 als auch
als auch 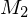 auf jeder Eingabe halten. Also entscheidet M ##L_1 \cup L_2#.
auf jeder Eingabe halten. Also entscheidet M ##L_1 \cup L_2#.Beweis: Sprachen 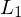 und
und 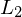 rekursiv aufzählbar, so auch
rekursiv aufzählbar, so auch 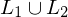 rekursiv aufzählbar
rekursiv aufzählbar
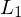 und
und 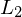 rekursiv aufzählbar, so auch
rekursiv aufzählbar, so auch 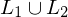 rekursiv aufzählbar
rekursiv aufzählbarBeweis anders, als bei anderen Sätzen, da 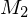 Eingabe evtl. akzeptiert, M dies aber nie feststellen kann, da
Eingabe evtl. akzeptiert, M dies aber nie feststellen kann, da 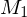 evtl. nicht terminiert (
evtl. nicht terminiert (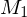 und
und 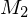 erkennen
erkennen 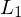 und
und 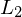 nur)
nur)
=> verwende parallele Simulation der beiden TMn (statt einer sequentiellen)
- M verwendet zwei Bänder: auf einem wird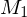 auf dem anderen
auf dem anderen 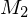 simuliert
simuliert
- M merkt sich in ihrem Zustand, den momentanen Zustand von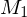 und
und 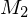
- pro Rechenschritt wird abwechselnd eine Rechenschritt von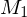 oder
oder 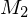 simuliert (ein bit gibt an, welche TM im aktuellen Rechenschritt simuliert wird)
simuliert (ein bit gibt an, welche TM im aktuellen Rechenschritt simuliert wird)
=> sichergestellt, dass M akzeptiert, falls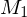 oder
oder 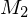 akzeptieren
akzeptieren
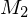 Eingabe evtl. akzeptiert, M dies aber nie feststellen kann, da
Eingabe evtl. akzeptiert, M dies aber nie feststellen kann, da 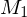 evtl. nicht terminiert (
evtl. nicht terminiert (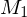 und
und 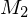 erkennen
erkennen 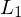 und
und 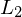 nur)
nur)=> verwende parallele Simulation der beiden TMn (statt einer sequentiellen)
- M verwendet zwei Bänder: auf einem wird
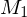 auf dem anderen
auf dem anderen 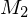 simuliert
simuliert- M merkt sich in ihrem Zustand, den momentanen Zustand von
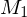 und
und 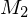
- pro Rechenschritt wird abwechselnd eine Rechenschritt von
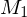 oder
oder 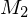 simuliert (ein bit gibt an, welche TM im aktuellen Rechenschritt simuliert wird)
simuliert (ein bit gibt an, welche TM im aktuellen Rechenschritt simuliert wird)=> sichergestellt, dass M akzeptiert, falls
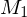 oder
oder 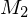 akzeptieren
akzeptieren Beweis: Sind 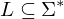 und
und 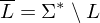 rekursiv aufzählbar, so ist L rekursiv.
rekursiv aufzählbar, so ist L rekursiv.
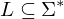 und
und 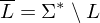 rekursiv aufzählbar, so ist L rekursiv.
rekursiv aufzählbar, so ist L rekursiv. Beispiel: Halteproblem
H ist rekursiv aufzählbar, wäre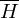 auch rekursiv aufzählbar, dann wäre H rekursiv
auch rekursiv aufzählbar, dann wäre H rekursiv 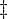
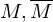 Maschinen, die L bzw.
Maschinen, die L bzw. 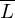 erkennen.
erkennen.
TM M' entscheidet L durch parallele Simulation von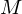 und
und 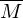 auf Eingabe w:
auf Eingabe w:
- M' akzeptiert w, sobald M akzeptiert
- M' verwirft w, sobald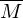 akzeptiert
akzeptiert
=> Terminierung: Da entweder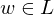 oder
oder  sicher
sicher
Folge aus dem Lemma: L ist nicht rekursiv gdw. mind. eine der beiden Sprache L oder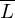 nicht rekursiv aufzählbar ist
nicht rekursiv aufzählbar ist
H ist rekursiv aufzählbar, wäre
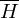 auch rekursiv aufzählbar, dann wäre H rekursiv
auch rekursiv aufzählbar, dann wäre H rekursiv 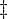
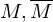 Maschinen, die L bzw.
Maschinen, die L bzw. 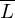 erkennen.
erkennen.TM M' entscheidet L durch parallele Simulation von
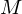 und
und 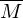 auf Eingabe w:
auf Eingabe w:- M' akzeptiert w, sobald M akzeptiert
- M' verwirft w, sobald
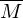 akzeptiert
akzeptiert=> Terminierung: Da entweder
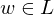 oder
oder  sicher
sicherFolge aus dem Lemma: L ist nicht rekursiv gdw. mind. eine der beiden Sprache L oder
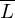 nicht rekursiv aufzählbar ist
nicht rekursiv aufzählbar istUnterschied Unterprogrammtechnik und Reduktion
Reduktion ist eine spezielle Variante der Unterprogrammtechnik, bei der nach dem Unterprogrammaufruf keine Manipulation der Ausgabe mehr möglich ist.
Insbesondere ist es nicht möglich nach dem Unterprogrammaufruf das Akzeptanzverhalten zu invertieren (macht bei Aufruf einer rek. aufz. Sprache als Unterprogramm auch wenig Sinn, da es auf Wörter, die nicht zur Sprache gehören, möglicherweise nicht terminiert)
Insbesondere ist es nicht möglich nach dem Unterprogrammaufruf das Akzeptanzverhalten zu invertieren (macht bei Aufruf einer rek. aufz. Sprache als Unterprogramm auch wenig Sinn, da es auf Wörter, die nicht zur Sprache gehören, möglicherweise nicht terminiert)
Was ist eine Reduktion?
Eine Reduktion ist eine Technik zum Nachweis, ob eine Sprache rekursiv bzw. rekursiv aufz. oder nicht rekursiv bzw. nicht rek. aufzb. ist.
Diese bildet die Eingabe eines Problems auf die Eingabe eines anderen Problems ab. Sie wird deshalb auch Eingabe-Eingabe-Reduktion bzw. Many-One-Reduktion genannt
Diese bildet die Eingabe eines Problems auf die Eingabe eines anderen Problems ab. Sie wird deshalb auch Eingabe-Eingabe-Reduktion bzw. Many-One-Reduktion genannt
Beweis: 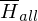 ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbar
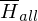 ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbarReduziere eine nicht rek. aufz. Sprache auf 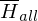 :
:
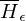 nicht rek. aufz. =>
nicht rek. aufz. => 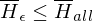 bzw. äquivalent
bzw. äquivalent 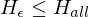
Konstruiere eine berechenbare Funktion f, die alle Ja/Nein-Instanzen von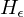 auf alle Ja/Nein-Instanzen von
auf alle Ja/Nein-Instanzen von  abbildet.
abbildet.
w Eingabe für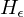
1.) Wenn w keine gültige GN, dann f(w)=w
2.) Wenn w=<M> GN einer TM, dann sei f(w) GN einer TM M* mit folgender Eigenschaft: M* ignoriert die Eingabe und simuliert M auf Eingabe
f ist offensichtlich berechenbar. Falls w keine GN ist, so gilt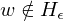 und
und 
Für w=<M> ist f(w)=<M*>:
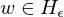 |
|
=> M hält auf Eingabe
=> M* hält auf jeder Eingabe
=> f(w)=<M*>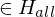
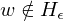
=> M hält nicht auf Eingabe
=> M* hält auf keiner Eingabe
=> f(w)=<M*>
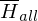 :
: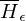 nicht rek. aufz. =>
nicht rek. aufz. => 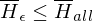 bzw. äquivalent
bzw. äquivalent 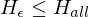
Konstruiere eine berechenbare Funktion f, die alle Ja/Nein-Instanzen von
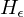 auf alle Ja/Nein-Instanzen von
auf alle Ja/Nein-Instanzen von  abbildet.
abbildet.w Eingabe für
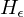
1.) Wenn w keine gültige GN, dann f(w)=w
2.) Wenn w=<M> GN einer TM, dann sei f(w) GN einer TM M* mit folgender Eigenschaft: M* ignoriert die Eingabe und simuliert M auf Eingabe

f ist offensichtlich berechenbar. Falls w keine GN ist, so gilt
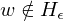 und
und 
Für w=<M> ist f(w)=<M*>:
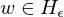 |
|=> M hält auf Eingabe

=> M* hält auf jeder Eingabe
=> f(w)=<M*>
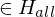
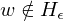
=> M hält nicht auf Eingabe

=> M* hält auf keiner Eingabe
=> f(w)=<M*>

Beweis:  ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbar
 ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbar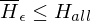
w Eingabe für
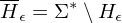
1.) Wenn w keine gültige GN ist, liegt w in
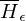 . Setze f(w)=w' mit w'
. Setze f(w)=w' mit w' 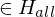
2.) Wenn w=<M>, so ist f(w)=<M'>. M' verhält sich auf Eingabe x wie folgt:
Falls |x|=i, simuliert M' die ersten i Schritte von M auf
 . Wenn M nach i Schritten hält, dann geht M' in eine Endlosschleife, ansonsten hält M'. (d.h. wenn M auf
. Wenn M nach i Schritten hält, dann geht M' in eine Endlosschleife, ansonsten hält M'. (d.h. wenn M auf  hält liegt M nicht in
hält liegt M nicht in 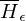 und M' darf damit nie halten).
und M' darf damit nie halten).f ist offensichtlich berechenbar.Falls w=<M> gilt:
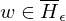
=> M hält nicht auf Eingabe

=>
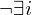 : M hält innerhalb von i Schritten auf
: M hält innerhalb von i Schritten auf 
=>
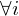 : M' hält auf allen Eingaben der Länge i
: M' hält auf allen Eingaben der Länge i=> f(w)=<M'>
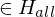
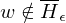
=> M hält auf Eingabe

=>
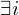 : M hält innerhalb von i Schritten auf
: M hält innerhalb von i Schritten auf 
=>
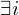 : M' hält nicht auf allen Eingaben der Länge i
: M' hält nicht auf allen Eingaben der Länge i=> f(w)=<M'>

Hilberts zehntes Problem
Beschreibe einen Algorithmus, der entscheidet, ob ein gegebenes Polynom mit ganzzahligen Koeffizienten eine ganzzahlige Nullstelle hat
N = {p / p ist ein Polynom mit einer ganzzahligen Nullstelle}
ist rekursiv aufzählbar:
Polynom p mit l Variablen (Wertbereich ist also abzählbar unendliche Menge aller l-Tupel mit Werten in Z: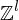 )
)
Zähle nun nacheinander alle l-Tupel auf und werte p für dieses Tupel aus
Akzeptiere falls Auswertung Null ergibt
=> N wird erkannt
ist nicht rekursiv:
Falls es obere Schranke für Absolutwerte der Nullstellen gebe, müsste man nur endlich viele l-Tupel aufzählen und N wäre rekursiv Dies gilt allerdings nur für Polynome mit einer Variablen:
Für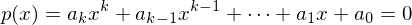 mit ganzzahligen Koeffizienten gitl:
mit ganzzahligen Koeffizienten gitl: 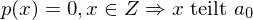 . Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.
. Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.
N = {p / p ist ein Polynom mit einer ganzzahligen Nullstelle}
ist rekursiv aufzählbar:
Polynom p mit l Variablen (Wertbereich ist also abzählbar unendliche Menge aller l-Tupel mit Werten in Z:
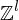 )
)Zähle nun nacheinander alle l-Tupel auf und werte p für dieses Tupel aus
Akzeptiere falls Auswertung Null ergibt
=> N wird erkannt
ist nicht rekursiv:
Falls es obere Schranke für Absolutwerte der Nullstellen gebe, müsste man nur endlich viele l-Tupel aufzählen und N wäre rekursiv Dies gilt allerdings nur für Polynome mit einer Variablen:
Für
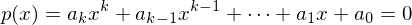 mit ganzzahligen Koeffizienten gitl:
mit ganzzahligen Koeffizienten gitl: 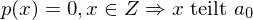 . Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.
. Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.Postsches Korrespondenzproblem
korrespondierende Folge: Folge von Dominos aus einer Menge K von Dominos, sodass oben und unten dasselbe Wort steht. (Folge soll aus mind. einem Domino bestehen und Dominos dürfen sich wiederholen)
Instanz des PKP: besteht aus einer Menge
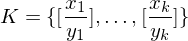
wobei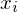 und
und 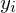 nichtleere Wörter über einem endlichen Alphabet
nichtleere Wörter über einem endlichen Alphabet 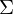 sind.
sind.
Es soll entschieden werden, ob es eine korrespondierende Folge von Indizes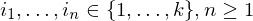 gibt, also eine Folge, sodass gilt
gibt, also eine Folge, sodass gilt
 .
.
=>PKP nicht rekursiv, aber rekursiv aufzählbar.
=>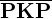 ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbar
(Reduziere dazu MPKP auf PKP und H auf MKPK daraus folgt dass man H auf PKP reduzieren kann)
Instanz des PKP: besteht aus einer Menge
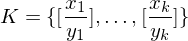
wobei
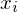 und
und 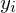 nichtleere Wörter über einem endlichen Alphabet
nichtleere Wörter über einem endlichen Alphabet 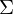 sind.
sind.Es soll entschieden werden, ob es eine korrespondierende Folge von Indizes
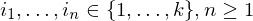 gibt, also eine Folge, sodass gilt
gibt, also eine Folge, sodass gilt  .
.=>PKP nicht rekursiv, aber rekursiv aufzählbar.
=>
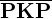 ist nicht rekursiv aufzählbar
ist nicht rekursiv aufzählbar(Reduziere dazu MPKP auf PKP und H auf MKPK daraus folgt dass man H auf PKP reduzieren kann)
Modifiziertes PKP
Modifikation: Startdomino 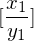 bestimmten, mit dem die korrespondierende Folge beginnen muss.
bestimmten, mit dem die korrespondierende Folge beginnen muss.
Instanz des MPKP: besteht aus einer geordneten Menge
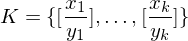
wobei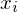 und
und 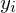 nichtleere Wörter über einem endlichen Alphabet
nichtleere Wörter über einem endlichen Alphabet 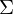 sind.
sind.
Es soll entschieden werden, ob es eine korrespondierende Folge von Indizes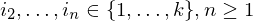 gibt, also eine Folge, sodass gilt
gibt, also eine Folge, sodass gilt
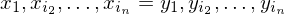 .
.
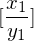 bestimmten, mit dem die korrespondierende Folge beginnen muss.
bestimmten, mit dem die korrespondierende Folge beginnen muss.Instanz des MPKP: besteht aus einer geordneten Menge
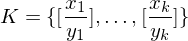
wobei
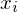 und
und 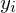 nichtleere Wörter über einem endlichen Alphabet
nichtleere Wörter über einem endlichen Alphabet 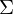 sind.
sind.Es soll entschieden werden, ob es eine korrespondierende Folge von Indizes
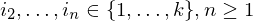 gibt, also eine Folge, sodass gilt
gibt, also eine Folge, sodass gilt 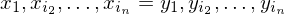 .
.Beweis: MPKP 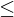 PKP
PKP
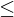 PKP
PKPDefiniere Funktion die Eingaben des MPKP auf Eingaben des PKP abbildet:
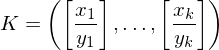 auf
auf 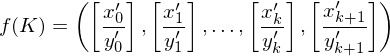
Führe Sonderzeichen #, $ ein, die nicht im Alphabet von MPKP enthalten sind
Füge nach jedem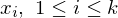 ein # ein
ein # ein
Füge vor jedem ein # ein
ein # ein
Füge Startdomino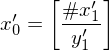 ein
ein
Füge Schlussstein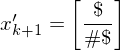 ein
ein
=> k Steine für MPKP, f(k) hat zwei Steine mehr
=> jede f(k) muss mit $ | #$ aufhören: egal was man legt, man muss oben mit # aufhören und unten mit nicht-# aufhören
=> jede Lösung muss mit Startdomino beginnen: einzige Möglichkeit oben mit # anzufangen
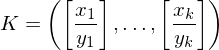 auf
auf 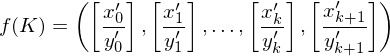
Führe Sonderzeichen #, $ ein, die nicht im Alphabet von MPKP enthalten sind
Füge nach jedem
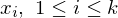 ein # ein
ein # einFüge vor jedem
 ein # ein
ein # einFüge Startdomino
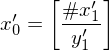 ein
einFüge Schlussstein
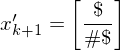 ein
ein=> k Steine für MPKP, f(k) hat zwei Steine mehr
=> jede f(k) muss mit $ | #$ aufhören: egal was man legt, man muss oben mit # aufhören und unten mit nicht-# aufhören
=> jede Lösung muss mit Startdomino beginnen: einzige Möglichkeit oben mit # anzufangen
Beweis: MPKP  PKP II
PKP II 
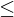 PKP II
PKP II 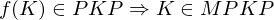
Sei 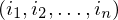 eine PKP Lösung minimaler Länge für f(K).
eine PKP Lösung minimaler Länge für f(K).
1.) Die Lösung beginnt und endet mit Anfangsstein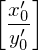 bzw. Schlussstein
bzw. Schlussstein 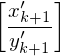 weil nur diese mit demselben Zeichen beginnen/enden
weil nur diese mit demselben Zeichen beginnen/enden
2.) Der Anfangsstein kann nicht in der Mitte vorkommen, da sonst im oberen Wort zwei # aufeinanderfolgen würden, was im unteren unmöglich ist.
3.) Der Schlussstein ist der letzte Stein, da sonst $ vorher auftreten würde und wir die korrespondierende Folge nach dem ersten Vorkommen des $-Zeichen abschneiden könnten und damit eine kürzere gefunden hätten.
Die PKP-Lösung von f(K) hat also die Struktur:

Daraus ergibt sich folgende MPKP-Lösung für K:
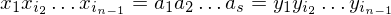
Es gilt also: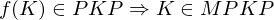
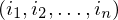 eine PKP Lösung minimaler Länge für f(K).
eine PKP Lösung minimaler Länge für f(K).1.) Die Lösung beginnt und endet mit Anfangsstein
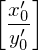 bzw. Schlussstein
bzw. Schlussstein 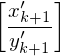 weil nur diese mit demselben Zeichen beginnen/enden
weil nur diese mit demselben Zeichen beginnen/enden2.) Der Anfangsstein kann nicht in der Mitte vorkommen, da sonst im oberen Wort zwei # aufeinanderfolgen würden, was im unteren unmöglich ist.
3.) Der Schlussstein ist der letzte Stein, da sonst $ vorher auftreten würde und wir die korrespondierende Folge nach dem ersten Vorkommen des $-Zeichen abschneiden könnten und damit eine kürzere gefunden hätten.
Die PKP-Lösung von f(K) hat also die Struktur:

Daraus ergibt sich folgende MPKP-Lösung für K:
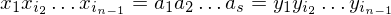
Es gilt also:
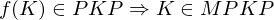
Simulation einer TM durch Dominos
Gegeben sei die Eingabe (<M>,w) für H. Konstruiere berechnbare Funktion f als Menge M von Dominos M=f(<M>,w). Bilde ungültige Eingaben für H auf ungültige Eingaben für MPKP ab.
1.) Startdomino: Startkonfiguration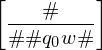
2.) Kopierdominos: für alle
für alle 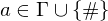
3.) Überführungssteine: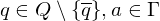
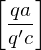 falls
falls 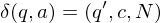
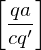 falls
falls 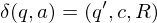
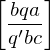 falls
falls 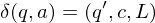
1.) Startdomino: Startkonfiguration
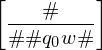
2.) Kopierdominos:
 für alle
für alle 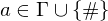
3.) Überführungssteine:
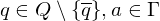
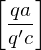 falls
falls 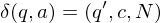
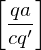 falls
falls 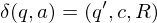
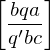 falls
falls 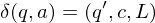
Korrektheit 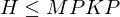 durch Dominos Teil 1
durch Dominos Teil 1
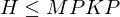 durch Dominos Teil 1
durch Dominos Teil 11.) M hält auf w => 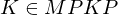
Dann entspricht die Rechnung von M einer endlichen Konfigurationsfolge: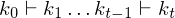 mit
mit 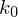 Start- und
Start- und 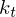 Endkonfiguration im Zustand
Endkonfiguration im Zustand 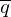
Man kann nun nach und nach Kopier- und Überführungsdominos legen, sodass der untere String die vollständige Konfigurationsfolge von M enthält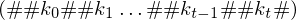 und der obere String ein Präfix des unteren ist
und der obere String ein Präfix des unteren ist 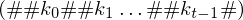
Durch Hinzufügen der Löschdominos kann Rückstand des unteren ausgeglichen werden. Danach sind sie identisch bis auf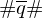 .
.
Durch hinzufügen des Abschlussdominos sind sie identisch: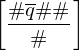
Wenn M auf w hält gilt also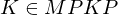
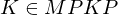
Dann entspricht die Rechnung von M einer endlichen Konfigurationsfolge:
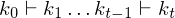 mit
mit 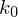 Start- und
Start- und 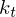 Endkonfiguration im Zustand
Endkonfiguration im Zustand 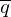
Man kann nun nach und nach Kopier- und Überführungsdominos legen, sodass der untere String die vollständige Konfigurationsfolge von M enthält
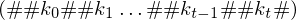 und der obere String ein Präfix des unteren ist
und der obere String ein Präfix des unteren ist 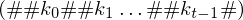
Durch Hinzufügen der Löschdominos kann Rückstand des unteren ausgeglichen werden. Danach sind sie identisch bis auf
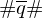 .
.Durch hinzufügen des Abschlussdominos sind sie identisch:
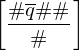
Wenn M auf w hält gilt also
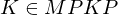
Korrektheit 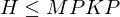 durch Dominos Teil 2
durch Dominos Teil 2
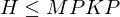 durch Dominos Teil 2
durch Dominos Teil 2M hält nicht auf w => 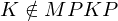
Nehme zum Widerspruch an, dass M nicht auf w hält, aber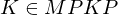 .
.
Nehme also an, dass eine korrespondierende Folge existiert.
1.) Mit Kopier- und Übergangsdominos entsteht bei Einhaltung der Übereinstimmung des oberen und unteren Strings die Konfigurationsfolge von M auf w. (Der obere String folgt dabei dem unteren String)
2.) Irgendwann muss auch der Abschluss- oder ein Löschdomino vorkommen. Diese enthalten jedoch im oberen Wort den Zustand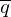 . Das Hinzufügen dieses Dominos verletzt die Übereinstimmung der beiden Strings, da im unteren String nie der Stoppzustand erreicht wird, da die Rechnung nicht terminiert. (Widerspruch zur Annahme, dass eine korrespondierende Folge existiert.)
. Das Hinzufügen dieses Dominos verletzt die Übereinstimmung der beiden Strings, da im unteren String nie der Stoppzustand erreicht wird, da die Rechnung nicht terminiert. (Widerspruch zur Annahme, dass eine korrespondierende Folge existiert.)
Nehme zum Widerspruch an, dass M nicht auf w hält, aber
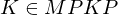 .
.Nehme also an, dass eine korrespondierende Folge existiert.
1.) Mit Kopier- und Übergangsdominos entsteht bei Einhaltung der Übereinstimmung des oberen und unteren Strings die Konfigurationsfolge von M auf w. (Der obere String folgt dabei dem unteren String)
2.) Irgendwann muss auch der Abschluss- oder ein Löschdomino vorkommen. Diese enthalten jedoch im oberen Wort den Zustand
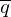 . Das Hinzufügen dieses Dominos verletzt die Übereinstimmung der beiden Strings, da im unteren String nie der Stoppzustand erreicht wird, da die Rechnung nicht terminiert. (Widerspruch zur Annahme, dass eine korrespondierende Folge existiert.)
. Das Hinzufügen dieses Dominos verletzt die Übereinstimmung der beiden Strings, da im unteren String nie der Stoppzustand erreicht wird, da die Rechnung nicht terminiert. (Widerspruch zur Annahme, dass eine korrespondierende Folge existiert.)Beweis: WHILE ist Turing-mächtig
Jede TM kann durch RAM mit konstant vielen Registern mit eingeschränktem Befehlssatz simuliert werden(LOAD,CLOAD,STORE,CADD,CSUB,GOTO, if c(0)!=0 GOTO, END)
Sei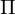 ein RAM-Programm, dass aus l Zeilen und k Registern für natürliche Zahlen besteht
ein RAM-Programm, dass aus l Zeilen und k Registern für natürliche Zahlen besteht
1.) Jede Zeile des RAM-Programms wird in eine WHILE Programm transformiert (Zeile i ist im WHILE Programm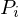 )
)
dazu: Inhalt von Register c(i) in Variable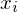
- bei k Registern also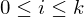
- Befehlszähler in Variable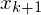 realisiert
realisiert
-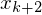 Variable mit initialem Wert 0
Variable mit initialem Wert 0
2.) Füge WHILE-Programme Pi' zu einem großen Programm P zusammen:
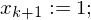
WHILE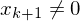 DO
DO
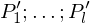
END Semantik: Falls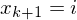 führe
führe 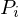 aus.
aus.
Das WHILE-Programm berechnet also dieselbe Funktion wie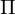
Sei
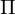 ein RAM-Programm, dass aus l Zeilen und k Registern für natürliche Zahlen besteht
ein RAM-Programm, dass aus l Zeilen und k Registern für natürliche Zahlen besteht1.) Jede Zeile des RAM-Programms wird in eine WHILE Programm transformiert (Zeile i ist im WHILE Programm
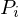 )
)dazu: Inhalt von Register c(i) in Variable
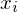
- bei k Registern also
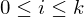
- Befehlszähler in Variable
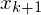 realisiert
realisiert-
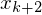 Variable mit initialem Wert 0
Variable mit initialem Wert 02.) Füge WHILE-Programme Pi' zu einem großen Programm P zusammen:
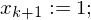
WHILE
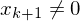 DO
DO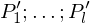
END Semantik: Falls
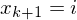 führe
führe 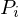 aus.
aus. Das WHILE-Programm berechnet also dieselbe Funktion wie
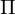
LOOP-Programme
ersetze WHILE durch LOOP-Schleife:
LOOP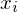 DO P END (
DO P END (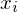 darf nicht in P vorkommen!)
darf nicht in P vorkommen!)
=> P wird sooft ausgeführt, wie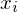 es vorgibt
es vorgibt
=> jedes LOOP-Konstrukt kann durch ein WHILE-Konstrukt ersetzt werden, aber nicht umgekehrt
=> LOOP-Programme terminieren immer, da man bei Eintritt in LOOP-Schleife weiß, wie oft diese ausgeführt wird (mit WHILE kann man dagegen Endlosschleifen konstruieren) => nicht alle Funktionen, die auf TM berechenbar sind, sind es auch LOOP-berechenbar
=> LOOP ist nicht TM-mächtig (Möglichkeit der Nicht-Terminierung ausgeschlossen)
Beweis: (berechenbare totale) Funktion gefunden, die von einer TM berechnet werden kann nicht aber durch ein LOOP-Programm:
Ackermann-Funktion
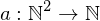
A(0,n) = n+1 für n >=0
A(m+1,0) = A(m,1) für m>=0
A(m+1,n+1) = A(m,A(m+1,n)) für m,n >=0
LOOP
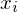 DO P END (
DO P END (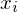 darf nicht in P vorkommen!)
darf nicht in P vorkommen!)=> P wird sooft ausgeführt, wie
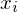 es vorgibt
es vorgibt=> jedes LOOP-Konstrukt kann durch ein WHILE-Konstrukt ersetzt werden, aber nicht umgekehrt
=> LOOP-Programme terminieren immer, da man bei Eintritt in LOOP-Schleife weiß, wie oft diese ausgeführt wird (mit WHILE kann man dagegen Endlosschleifen konstruieren) => nicht alle Funktionen, die auf TM berechenbar sind, sind es auch LOOP-berechenbar
=> LOOP ist nicht TM-mächtig (Möglichkeit der Nicht-Terminierung ausgeschlossen)
Beweis: (berechenbare totale) Funktion gefunden, die von einer TM berechnet werden kann nicht aber durch ein LOOP-Programm:
Ackermann-Funktion
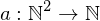
A(0,n) = n+1 für n >=0
A(m+1,0) = A(m,1) für m>=0
A(m+1,n+1) = A(m,A(m+1,n)) für m,n >=0
Flashcard set info:
Author: hemag
Main topic: Mathematik
Topic: Berechenbarkeit
Published: 16.03.2010
Card tags:
All cards (76)
no tags



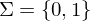 . Wofür steht
. Wofür steht 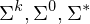 ? Was ist eine Sprache über dem Alphabet
? Was ist eine Sprache über dem Alphabet 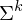 : Menge der Wörter der Länge k über dem Alphabet
: Menge der Wörter der Länge k über dem Alphabet 
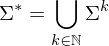 : Kleenescher Abschluss. Alle Wörter über
: Kleenescher Abschluss. Alle Wörter über 
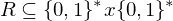 mit
mit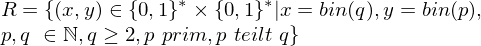
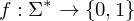
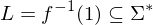 ist Menge der Eingaben mit Ja-Antwort und ist Teilmende der Wörter über
ist Menge der Eingaben mit Ja-Antwort und ist Teilmende der Wörter über 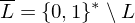
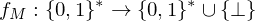

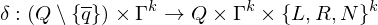
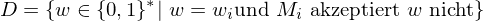
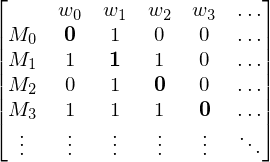
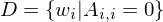
 Tm, die L entscheidet. Man erhält TM
Tm, die L entscheidet. Man erhält TM 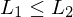 ), wenn es eine berechenbare Funktion
), wenn es eine berechenbare Funktion 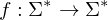 gibt, sodass für alle
gibt, sodass für alle 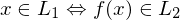

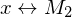 akz.
akz. 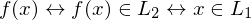

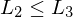 , folgt
, folgt 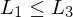 für beliebige Sprachen
für beliebige Sprachen 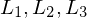 .
.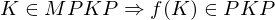
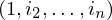 eine MPKP-Lösung also
eine MPKP-Lösung also 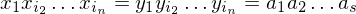 für gewählte Symbole aus
für gewählte Symbole aus 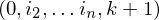 eine PKP-Lösung für f(K), denn
eine PKP-Lösung für f(K), denn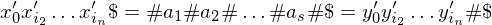 .
.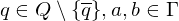
 falls
falls 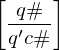 falls
falls 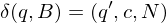
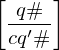 falls
falls 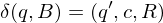
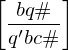 falls
falls 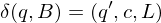
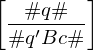 falls
falls 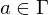
 und
und 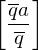
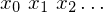
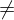
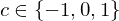 :
: 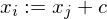
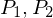 WHILE-Programme:
WHILE-Programme: 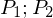
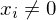 DO P END
DO P END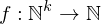
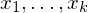 enthalten
enthalten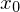 ergibt
ergibt implementieren.
implementieren.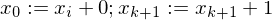
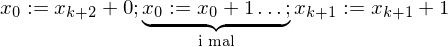
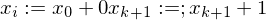
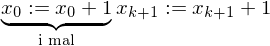
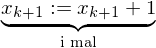
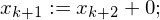
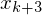 Hilfsvariable help
Hilfsvariable help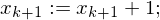 (b:=b+1)
(b:=b+1)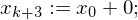 (help := c(0))
(help := c(0))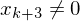 DO (while help != 0 do)
DO (while help != 0 do)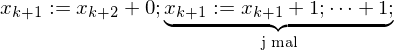 (b:=j)
(b:=j)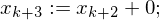 (help :=0)
(help :=0)