Bei einer Funktion f gilt für alle 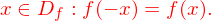
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
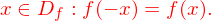
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die (Achsen-)Symmetrie des Schaubildes von f zur y-Achse
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion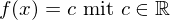
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
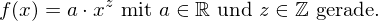
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
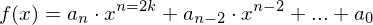
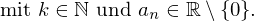
- Die Kosinusfunktion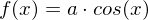 mit beliebigem
mit beliebigem
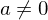 .
.
- Die Nullfunktion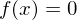 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.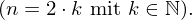
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion
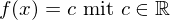
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
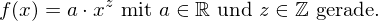
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
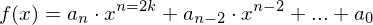
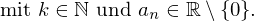
- Die Kosinusfunktion
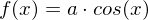 mit beliebigem
mit beliebigem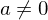 .
.- Die Nullfunktion
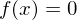 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.
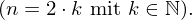
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Bei einer Funktion f gilt für alle 
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.

Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die Punktsymmetrie des Schaubildes von f zum Ursprung
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität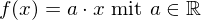 oder
oder
allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
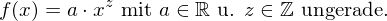 .
.
Hierzu zählt auch die Kehrwertfunktion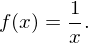
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
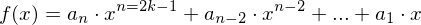
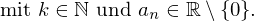
- Die Sinusfunktion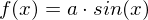 mit beliebigem
mit beliebigem
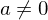 .
.
- Die Nullfunktion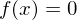 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.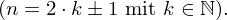
Beachte, dass man die entsprechende Funktion als "ungerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede Proportionalität
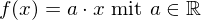 oder
oder allg. Potenzfktn. mit ungerader, ganzzahliger Hochzahl
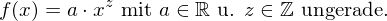 .
. Hierzu zählt auch die Kehrwertfunktion
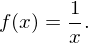
- Jede ganzrationale Funktion mit ausschließlich ungeraden
"x-Potenzen"
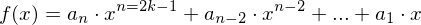
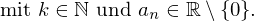
- Die Sinusfunktion
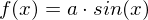 mit beliebigem
mit beliebigem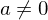 .
.- Die Nullfunktion
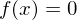 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte jeweils Zahl und Gegenzahl."
Ungerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2 abzüglich oder zuzüglich 1.
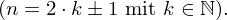
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Überprüfe, ob das Schaubild der Funktion 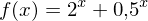 punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
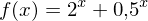 punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.
punktsymmetrisch zum Ursprung oder symmetrisch zur y-Achse ist.Die Funktion f ist für alle reelen Zahlen definiert. Für jedes x gilt:
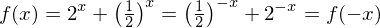
Somit ist die Funktion f gerade und das zugehörige Schaubild ist symmetrisch zur y-Achse.

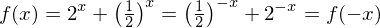
Somit ist die Funktion f gerade und das zugehörige Schaubild ist symmetrisch zur y-Achse.

Tags: Funktion, Symmetrie
Source:
Source:
Flashcard set info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009
Card tags:
All cards (47)
Ableitung (10)
Änderungsrate (9)
Anwendung (2)
Begriffe (17)
Definitionsmenge (1)
Extremstelle (2)
Funktion (8)
ganzrational (5)
Gerade (13)
Grad (1)
h-Methode (6)
hinreichend (3)
Intervalle (1)
Normale (2)
notwendig (2)
Nullstelle (5)
Produktform (3)
Sattelpunkt (3)
Schnittwinkel (1)
Sekante (1)
Sekantensteigung (1)
Steigungswinkel (3)
Streckung (1)
Symmetrie (3)
Tangente (7)
Terassenpunkt (3)
Verschiebung (7)
Wertemenge (1)



